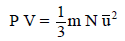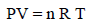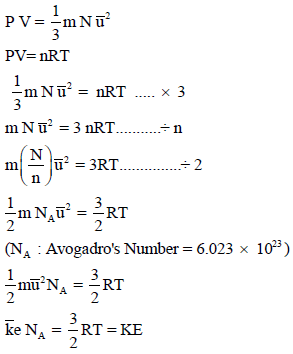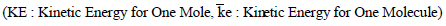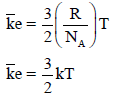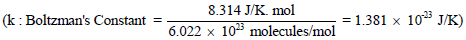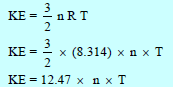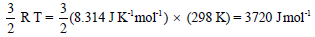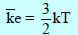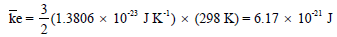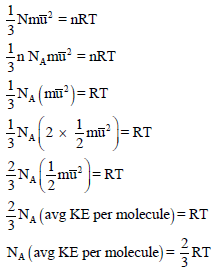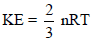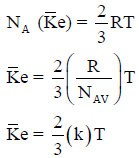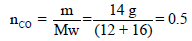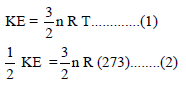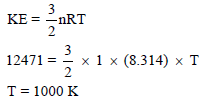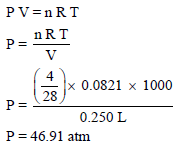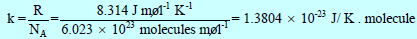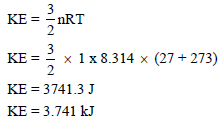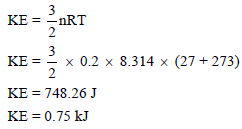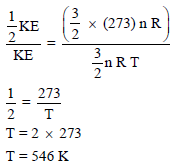العلاقة بين الطاقة الحركية ودرجة الحرارة Relation between KE , T

الطاقة الحركية ودرجة الحرارة Kinetic Energy and Temperature

– المعادلة الأساسية للنظرية الحركية للغازات:

حيث أن:

N: عدد جزيئات الغاز

m: كتلة الجزئ في حيز ما

ˉu²: متوسط مربع سرعة الجزئ الواحد.

– القانون العام للغازات:

– من خلال المعادلة الأساسية للنظرية الحركية للغازات والقانون العام للغازات يمكن استنتاج العلاقة بين الطاقة الحركية ودرجة الحرارة كما يلي:

– بالتالي فإنه لحساب الطاقة الحركیة لعدد n من المولات فإن:

ومنه فإن الطاقة الحركیة لكمیة محددة من الغاز لا تعتمد على ضغطه ، ولا حجمه ولا نوعه بل تعتمد فقط على درجة حرارته.

– إذا اخترنا القيمة (8.314 JK^-1mol^-1) قيمة ثابت الغاز R ، فإن إسهام الحركة الانتقالية في طاقة جزئ جرامي واحد من أي غاز مثالي عند درجة حرارة 25 C^o تصبح:

– يمكن التعبير عن متوسط طاقة الحركة لجزيء واحد من غاز كما یلي:

ثابت بولتزمان Boltzman’s Constant

– ونظراً لأن معظم دراستنا اللاحقة تتعلق بطاقات الجزیئات والذرات المنفردة فمن الأفضل أن ندخل ثابتاً جدیداً یعرف بثابت بولتزمان Boltzman’s Constant ویرمز له بالرمز (k) وتكون قیمته كما یلي:

– ثابت بولتزمان ھو ثابت الغاز للجزيء الواحد، وبذلك تكون متوسط طاقة الحركة للجزيء الواحد تساوي:

– ويكون متوسط طاقة الحركة لجزئ ما عند درجة حرارة (25 C^o) مساوية:

طريقة إثبات أخرى للعلاقة بين الطاقة الحركية ودرجة الحرارة

من المعادلة نجد أن: درجة الحرارة تتناسب تناسباً طردياً مع متوسط طاقة الحركة الجزيئية.

– متوسط الطاقة الحركية لعدد (n) من مولات الغازات:

– متوسط الطاقة الحركية لجزئ من الغاز:

أمثلة محلولة على العلاقة بين الطاقة الحركية ودرجة الحرارة

مثال (1): ما مقدار طاقة الحركة عند الظروف القياسية لكل من:

(أ) 0.1 mol من غاز ما

(ب) 1 mol من غاز ما

الحل:

نتبع العلاقة التالية :

مثال (2): أوجد طاقة حركة مول واحد من غاز مثالي عند (27 C^o) بوحدة KJ

الحل:

مثال (3): أوجد طاقة حركة (0.2 mol) من غاز مثالي عند (27 C^o) بوحدة KJ

الحل:

مثال (4): أوجد الطاقة الحركية لكتلة مقدارها (14 g) من غاز (CO) عند (25 Co) بوحدة الجول (J) (الكتلة الذرية: C=12 , O = 16)

الحل:

نوجد أولاً عدد المولات كما یلي :

ثم نوجد الطاقة الحركیة كما یلي :

مثال (5): أوجد درجة الحرارة بوحدة الكلفن (K)لكي تكون للطاقة الحركية لمول من غاز الأكسجين نصف قيمتها عند الظروف القياسية.

الحل:

نكون معادلتين إحداهما في درجة حرارة (T) والأخرى في درجة حرارة 298 K (الحرارة في الظروف القياسية).

وبقسمة المعادلة (2) على المعادلة (1) نحصل علي:

مثال (6): أحسب ضغط (4 g) من غاز النيتروجين (N₂) إذا علمت أن حجمه يساوي ( 250 ml) وأن الطاقة الحركية (KE) لمول واحد منه تساوي 12471 J/mol