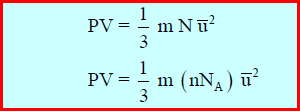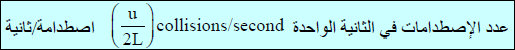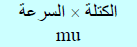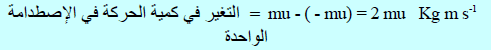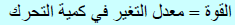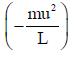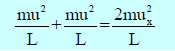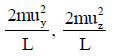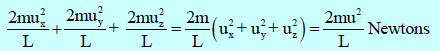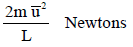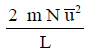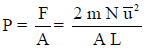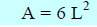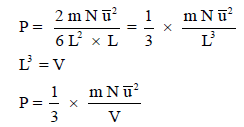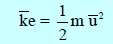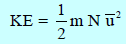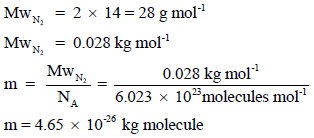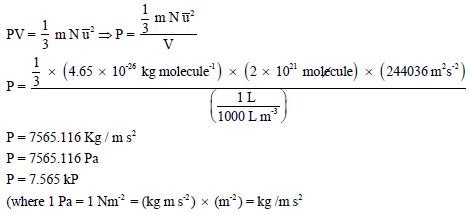اشتقاق المعادلة الحركية للغازات Kinetic Equation of Gases

في هذا الموضوع بإذن الله سوف نتناول كيفية اشتقاق أو استنتاج المعادلة الأساسية للنظرية الحركية Fundamental Equation of the Kinetic Theory أو فيما يعرف بالمعادلة الحركية للغازات Kinetic Equation of Gases

المعادلة الأساسية للنظرية الحركية للغازات

(1) من الممكن بناءً على فروض النظریة الحركیة للغازات إیجاد علاقة تربط بين ضغط الغاز المثالي (P) وكتلة الغاز (m) وسرعة الجزيئات (u)

(2)نفترض أن لدينا غاز محبوس في إناء مكعب الشكل طول ضلعه (L)وحجمه ومساحة كل جدار له (L²).

(3) يحتوي المكعب على (N) من الجزئيات ، كتلة الجزيء الواحد منها (m) وسرعته (u) عند درجة حرارة ثابتة.

(4) ووفقاً للنظریة الحركیة للغاز فإن الجزیئات تتحرك عشوائیة في جمیع الإتجاھات· (تتحرك في كل اتجاه).

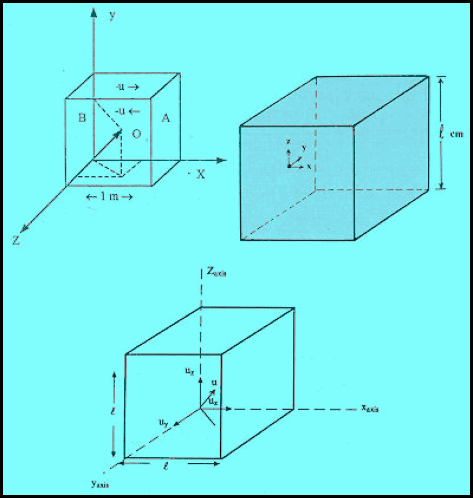
(5) ولتبسیط الاشتقاق فإنه یمكن تحلیل السرعة (u)للجزیئات في أي لحظة في ثلاث اتجاھات محوریة (x, y, z)متعامدة على بعضھا كما ھو مبین بالشكل التالي:

وبالتالي فـ (1/3) من الجزيئات أي(1/3)N يتحرك في اتجاه الإحداثي X ، ومثله في اتجاه الإحداثي Y وآخر في اتجاه Zوھذا التبسیط لا غبار علیه حيث یمكن تحلیلھا الى مكوناتھا في اتجاه ثلاثة محاور عمودیة هي Y, Z)(X

(6) ینتج ضغط الغاز على أي جدار من جدران الإناء نتيجة الاصطداماتالتي تقوم بها الجزيئات على هذا الجدار.

ومن المعروف أن القوة الناتجة عن كل اصطدامه یمكن حسابھا من معرفتنا أن القوة عبارة عن معدل تغیر كمیة الحركة مع الزمن . ومن معرفتنا لهذه المبادئ يمكن أن نشتق المعادلة العامة للغاز المثالي.

(7) ولنرمز الى السرعات في الاتجاهات الثلاث بالرموز (u_x , u_y, u_z) ومتوسط الجذر التربيعي للسرعة u᷆² ويسمى باللغة الأنجليزية Root Mean Square Velocity

حساب عدد الاصطدامات لجزيء

(8) وإذا تصورنا جزيئاً واحداً یصطدم بجدار المكعب (A) أي في اتجاه المحور الإحداثي (x)وبسرعة قدرها (u m/s)هذا الجزيء المتحرك في هذا الاتجاه سيصطدم بالجدار المظلل كما قطع مسافة (2 L cm)خلال مساره وذلك لأنه بعد الاصطدام لابد أن يقطع مسافة (L) ليصل الى الجدار المقابل ثم يعود مسافة (L) ليصطدم مرة أخرى بالجدار المظلل أي يقطع مسافة (2 L) ليصطدم مرة أخرى بنفس الجدار.

(9) فإذا كان الجزيء يتحرك بسرعة (u m/s)فمعنى ذلك أنه خلال ثانية واحدة يكون قد قطع مسافة (u cm).

وبالتالي فالزمن الذي یمر قبل أن یقوم الجزيء بعمل اصطدامه ثانية مع نفس وجه الصندوق تحدده العلاقة:

(10) وبالتالي فإن عدد الإصطدامات التي سیحدثھا على الجدار المظلل في الثانیة الواحدة (في وحدة الزمن) یكون مساویاً للمسافة التي قطعھا في الثانیة الواحدة مقسوماً على المسافة التي یقطعھا لیحدث الإصطدامة (مقلوب التعبیر السابق)

وبفرض أن عملیة الإصطدام مرنة فإن الجزيء سوف یرتد في الإتجاه المعاكس بنفس السرعة السابقة (لأن الاصطدام مرن) مع عكس الإشارة (- u)وبالتالي فإن كمیة تحرك الجزيء (كمیة الحركة للجزيء) قبل اصطدامه بالسطح (الجدار A) في اتجاه المحور x تساوي:

وكمية الحركة بعد الاصطدام بالجدار = – mu

(11) إذا التغير في كمية التحرك للجزئ الواحد في كل اصطدامه على السطح (A)(التغير في كمية الحركة للإصطدام الواحد)

والآن فإن القوة التي یؤثر بھا جسیم وحید على ذلك الوجه من الصندوق یحددھا معدل التغیر في كمیة التحرك الذي یمارسه الجسیم (القانون الثاني لنیوتن):

ولھذا سیكون التغیر في كمیة التحرك لكل ثانیة بالنسبة لجزيء واحد للسطح الواحد في الذھاب یساوي

(12) وعند الإیاب سوف یتعرض السطح (B) المقابل بحیث یصبح التغیر في كمیة التحرك لكل ثانیة لنفس الجزيء ھو:

(13) وبالتالي فإن معدل التغیر في كمیة التحرك لكل ثانیة للجزيء على السطحین المتقابلين (A, B) على طول المحور X يساوي:

(14) وبالمثل یمكن حساب التغیر في كمیة التحرك لنفس الجزيء في اتجاه المحورین الآخرين(y, z)يساوي على التوالي:

(15) ویصبح التغیر الكلي في كمیة التحرك بالنسبة للأوجه الستة للمكعب ھو:

(16) وطبقاً لقانون نیوتن للحركة:

فإن معدل التغیر في كمیة التحرك یكون مساویاً للقوة المؤثرة، والقوة الناتجة عن ضربات الجزيء الواحد ھي:

(17) القوة الكلية الناتجة عن عدد (N)من الجزيئات هي:

(18) وحیث أن الضغط یعرف بأنه القوة الدافعة على وحدة المساحات:

حيث أن (P) الضغط ، A مساحة سطح الوجة الواحد من المكعب وحيث أن مساحة أوجه المكعب الست هي:

وبالتالي:

وتعرف ھذه المعادلة بالمعادلة الحركیة للغازات المثالیة.

– یمكن كتابة التعبیر الأخیر لضغط الغاز بصورة بدیلة، حیث:

(mN) هي الكتلة الكلية للغاز

(V)هي الحجم الكلي

(d)الكثافة وتساوي mN/V

وتصبح المعادلة كما يلي:

معادلة الطاقة الحركية للجزئيات

الصيغة الرياضية

K᷆e: الطاقة الحركية بوحدة (J)لجزئ واحد من الغاز

m: كتلة الجزئ الواحد بوحدة الكيلو جرام (Kg)

u᷆² : متوسط مربع سرعة الجزيء بوحدة (m²/s²)

– الطاقة الحركية لعدد (N) من الجزيئات هي:

مثال محلول على المعادلة الحركية للغازات

احسب الضغط بوحدة kPa المبذول بواسطة (2 x 10²¹ molecules) من غاز النيتروجين في وعاء حجمه (1 L)علماً بأن متوسط مربع السرعة لهذة الجزيئات هو (244036m²/s²)(الكتلة الذرية لعنصر النيتروجين =(14

الحل:

نحسب أولاً كتلة ا لجزيء الواحد من غاز النیتروجین بوحدة Kg:

وبتطبیق المعادلة الأساسیة للنظریة الحركیة للغازات:

المراجع:

أسس الكيمياء العامة والفيزيائية – الجزء الأول. عمر بن عبد الله الهزازي ، قسم الكيمياء- كلية العلوم – جامعة أم القرى – المملكة العربية السعودية