الكيمياء العامة
اشتقاق قانون (بويل – شارل – جاى لوساك) من النظرية الحركية للغازات
يوضح هذا الموضوع كيف استطاعت النظرية الحركية الجزيئية للغازات تفسير قوانين الغازات مثل قانون بويل وقانون شارل وقانون جاى لوساك وسوف نستكمل باقى القوانين فى الموضوع القادم.
أولاً/ إثبات قانون بويل من خلال النظرية الحركية للغازات
– في البداية يمكنك مراجعة قانون بويل Boyle’s Law من خلال هذا الرابط.
– إن أهم خاصية ملفتة للنظر هي قابلية الغاز للانضغاط لذلك يجب أن تكون الجزيئات التي تم تصورها في النظرية الجزيئية الحركية دقيقة جداً ومتباعدة عن بعضها في الغاز بحيث يوجد هنالك وفرة في الحيز الفارغ بينها. فبهذه الطريقة فقط يمكن أن تحشر الجزئيات مع بعضها بعضاً بهذه السهولة. فأثناء تطاير هذه الجسيمات الدقيقة، تصطدم مع بعضها وبجدران الوعاء. وكل تصادم مع الجدار يمارس دفعة ضئيلة جداً. والتأثيرات المتراكمة للأعداد الضخمة في مثل هذه التصادمات كل ثانية على كل سنتيمتر مربع في الجدار تؤدي إلى ضغط الغاز.
– یعتمد الضغط على عاملین:
(1)عدد الجزيئات التي ترتطم بالجدران في وحدة الزمن
The number of molecules striking the walls per unit time
(2) مدى قوة اصطدام الجزیئات بالجدران
how vigorously the molecules strike the walls
– عند درجة حرارة ثابته فإن متوسط السرعة (Average speed) وقوة الإصطدامات (force of the collisions) تبقى نفسها . ويعتمد ضغط الغاز فقط على عدد الصدمات الجزيئية (Molecular collision) لكل وحدة مساحة من الجدار لكل ثانية، إذا أبقيت درجة الحرارة ثابتة لكى تتحرك الجزئيات بنفس السرعة المتوسطة . وعدد الصدمات يعتمد على الكثافة (عدد الجزيئات في وحدة الحجوم).
– عن خفض حجم الغاز فإن كثافته تزيد وبالتالي يزاد معدل التصادم فيزداد الضغط ومن هنا نشأت العلاقة العكسية بين الضغط والحجم (قانون بويل).
مثال توضيحي
– وبمثل ھذا النموذج للغاز في ذهننا نستطيع تفسير قانون بويل. فعندما نشطر حجم الغاز إلى نصفين فنحن نرص ضعف عدد الجزيئات في كل سنتيمتر مكعب (عندما ينقص الحجم لا يكون للجزيئات قدر كبير من حجم تتحرك فيه) كما أن هناك الآن على كل سنتيمتر مربع في الجدار جزيئات ضعف ما كان في السابق. ولذلك يجب أن يكون ضعف عدد تصادمات الجزيئات مع الجدران مع كل ثانية (تصطدم الجزيئات مع الجدران بتكرار أكثر) وبذلك فإن الجدران تستقبل صدمات أكثر لكل ثانية) وهذا يعنى أن الضغط يتضاعف (الضغط يكون أكبر في حجم أصغر) كما هو موضح بالشكل التالي:

– إذا كان تنصيف الحجم يضاعف الضغط ، عندئذ الضغط والحجم يتناسبان عكسياً مع بعضهما بعضاً، وهذة العبارة هي قانون بويل.
– أن الغاز المثالي كما تذكر يخضع لقانون بويل تماماً تحت كافة الظروف . وهذا يعنى أنه مهما كانت الجزئيات مرصوصة بإحكام ، سيكون دائماً من الممكن تنصيف حجمها بمضاعفة الضغط . والطريقة الوحيدة التى يمكن بها حدوث ذلك مرة بعد أخرى، ھي بالطبع إذا كان الغاز مكوناً من جسیمات لیس لها حجم بحيث أن الحجم كله عبارة عن حیز فراغ. ولكن الجزیئات الحقیقیة لھا أحجام محددة وهكذا لا يمكن لأي غاز حقیقي أن یخضع لقانون بویل تماماً، خاصة تحت ضغط عال.
إثبات قانون بويل رياضيًا من خلال النظرية الحركية للغازات
طبقاً للنظریة الحركیة للجزیئات تتناسب الطاقة الحركیة للجزیئات طردیاً مع درجة الحرارة المطلقة للغاز أي أن:
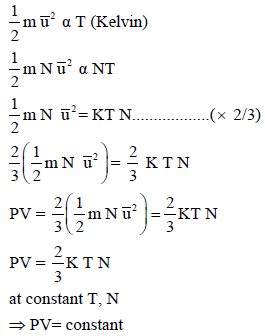
طريقة إثبات أخرى:
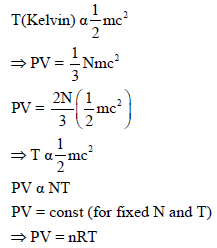
ثانياً/ إثبات قانون شارل من خلال النظرية الحركية للغازات
– في البداية يمكنك مراجعة قانون شارل Charle’s Law من خلال هذا الرابط.
– ینص ھذا القانون بأن الحجم یزداد عند رفع درجة الحرارة بشرط إبقاء الضغط ثابتاً.
– لقد رأينا للتو أن رفع درجة الحرارة يتسبب في جعل عدد أكثر من الجزيئات يصطدم بالجدار في كل ثانية (التأثير الناتج عن رفع درجة الحرارة بالنسبة لغاز هو زيادة متوسط طاقة الحركة للجزيئات)، ویتسبب أیضاً في جعل قوة صدمة الجزيئات مع الجدران تزداد بسب الزيادة في متوسط الطاقة الحركیة للجزیئات، بحیث یؤدي الى معدل أكبر في تغیر كمیة التحرك (عندما تتحرك الجزیئات وھي مزودة بطاقة أكبر فإنھا ترتطم بجدران الإناء الحاوي بتكرار أكثر وبنشاط أكثر محدثة بذلك ضغطاً أكبر، مما ینتج عنه زیادة في الضغط).
– والطریقة الوحیدة للمحافظة على ثبات الضغط هو تخفيض عدد الإصطدامات في الثانیة الواحدة مع كل سنتیمتر مربع من الجدار. وبالإمكان تحقیق هذا بالسماح للغاز بالتمدد فیتواجد عدد أقل من الجزيئات على كل سنتيمتر مربع من الجدار.
بتعبير آخر فالمحافظة على ضغط الغاز ثابتاً عندما نرفع درجة حرارته. علينا ان نسمح له بالتمدد وإشغال حجم أكبر. (وهذا التمدد يكون في الجدران المرنة حيث يتمدد الغاز لكى يشغل حجماً أكبر، وبذلك يحتفظ الغاز بالضغط الابتدائي ويستمر التمدد في حجم الوعاء حتى يعادل ضغط الغاز مع الضغط الثابت الخارجي.
مثال توضيحي
– الشكل التالي یوضح أنه إذا كان الضغط على البالون ثابتاً في حين ترفع درجة الحرارة ، فإن الغاز يمدد البالون إلى حجم أكبر، ويحدث فيه تعويض من الحركة الجزيئية الأكثر نشاطاً.

– الآن دعنا نتأمل فيما يحدث عند تبريد غاز ما. فإذا اتبعنا التعليل نفسه كما في الفقرة السابقة فإننا نجد أنه حتى نحافظ على ثبات الضغط عندما يبرد الغاز، فأنه يجب علينا إنقاص الحجم. فالجزيئات تتحرك ببطء أكثر فأكثر، والحيز بينها يصبح أقل تدريجياً.
– وفي آخر الأمر، تتكثف جمیع الغازات الحقیقیة لتكون سائلاً، عندما یتم تبریدھا ، لأن قوى التجاذب بین الجزیئات تسبب في نھایة الأمر اصطدامات “لزجة” . إلا أن الغاز المثالي لا یتكثف بغض النظر عن كمیة التبرید التي نقوم بها، ومن هنا فإن خاصية أخرى ” لجزیئات” الغاز المثالي ھي أنه لیس لدیھا قوى تجاذب بین جزیئیة. فالغاز المثالي إذاً مادة افتراضیة لیس لجزیئاتھا حجم ولا قوى تجاذب “بین جزیئیة”.
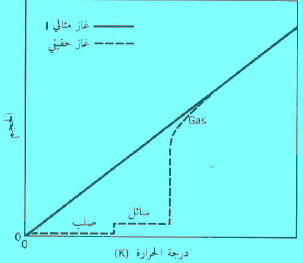
إثبات قانون شارل رياضيًا من خلال النظرية الحركية للغازات
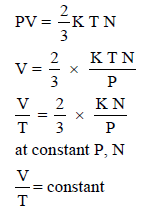
ثالثاً/ إثبات قانون جاي لوساك (أو آمونتونز) من خلال النظرية الحركية للغازات
– في البداية يمكنك مراجعة قانون جاى لوساك Gay-Lussac’s Law من خلال هذا الرابط.
– ينص قانون جاى لوساك على أن:
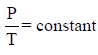
– ينص القانون أنه إذا أبقينا الحجم ثابتاً يتناسب الضغط مباشرة مع درجة الحرارة المطلقة. وبعبارة أخرى عندما تزداد درجة الحرارة يزداد الضغط أيضاً. فكيف بمقدورنا تفسير هذا من خلال النظرية الحركية للغازات؟
– بموجب النظرية الحركية يؤدي رفع درجة الحرارة إلى ازدياد متوسط الطاقة الحركية للجزيئات. وهكذا تتحرك الجزيئات بسرعة أعلى (بزيادة درجة الحرارة سوف يزداد متوسط الطاقة الحركية للجزيئات. مما يؤدي إلى زيادة في التغير في كمية التحرك عند جدران الوعاء الحاوي ثابت الحجم، والنتيجة هي زيادة في الضغط). وهذا يعني أنها ستصطدم بالجدار عدداً أكثر من المرات وأنه عند اصطدامها بالجدار سيكون متوسط قوة الصدمة أكبر. فتؤدي هذه العوامل إلى ازدياد الضغط.
– عادة ما يلاحظ هذا التأثير بالنسبة لإطار السيارة حيث يكون الغاز محصوراً في حجم ثايت تقريباً. ونتيجة لظروف الاحتكاك وانثنائية المطاط فإن الهواء داخل الإطار سوف تزداد درجة حرارته ويتعاظم الضغط.
المراجع – أسس الكيمياء العامة والفيزيائية – الجزء الأول.عمر بن عبد الله الهزازي ، قسم الكيمياء- كلية العلوم – جامعة أم القرى – المملكة العربية السعودية
المراجع – أسس الكيمياء العامة والفيزيائية – الجزء الأول.عمر بن عبد الله الهزازي ، قسم الكيمياء- كلية العلوم – جامعة أم القرى – المملكة العربية السعودية