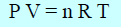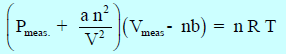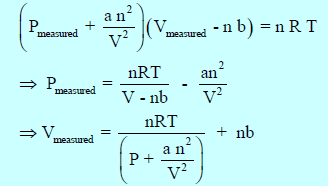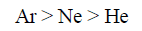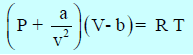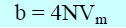معادلة الحالة فان در فالز لوصف حالة الغاز الحقيقي

معادلة الحالة لفان در فالز van der Waals Equation of State

– هي معادلة سميت باسم واضعها العالم الهولندي يوهانس ديديريك فان دير فالس. وهي معادلة الحالة تقريبية تصف حالة الغازات الحقيقية. تأخذ معادلة فان دير فالس في اعتبارها اختلاف الغاز الحقيقي عن الغاز المثالي .

– العلاقة التالية (القانون العام للغازات):

P V = n R T

لا تكون صحیحة إلا في الحالة المثالیة للغاز، أما في حالة الغاز الحقیقي (الغاز الذي یحید عن السلوك المثالي) فإنھا لا تكون صحیحة (خاصة تحت ضغط عال ودرجة حرارة منخفضة) إلا بعد أخذ تصحیحات فان در فالز في الإعتبار

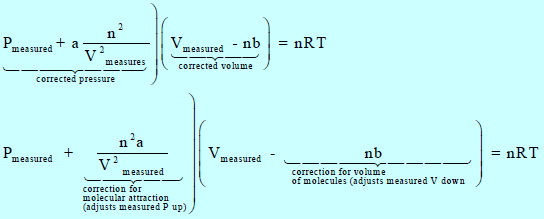
– إحدى طرق تحسین الدقة ھي تعدیل قانون الغاز المثالي بحیث تؤخذ في الإعتبار العوامل التي تسبب في جعل الغاز الحقیقي مختلفاً (یحید) عن الغاز المثالي.

وبالتعویض بھا في معادلة الغاز المثالي:

یعطینا:

وباختصار فإن المعادلة النھائیة:

وتعرف ھذه المعادلة بمعادلة فان درفالز للغاز الحقیقي  Van der Waals Equation of State for A real Gas حيث (a, b): ثابتا فان درفالز، ویعتمدان في قیمتھما على نوع الغاز وعلى الوحدات المستخدمة لقیاس الحجم والضغط، ویتم إیجاد قیمتھما تجریبیاً.

– في معادلة فان درفالز تمثل كل الرموز قیماً مقاسة، وھي أكثر تعقیداً من معادلة الغاز P V = n R T ولكنھا تصلح جیداً للعدید من الغازات وفي مجالات واسعة نسبیاً من درجات الحرارة والضغط.

– معادلة فان درفالز بجانب أنھا ریاضیاً بسیطة جداً إلا أنھا أعطت تفسیراً لسلوك الغازات الحقیقیة على المستوى الجزیئ وحیودھا عن السلوك المثالي الذي یخضع للعلاقة P V = n R T

وبالتالي فإنه لحساب ضغط الغاز الحقیقي P_measured أو حجمه الحقيقي V_measured:

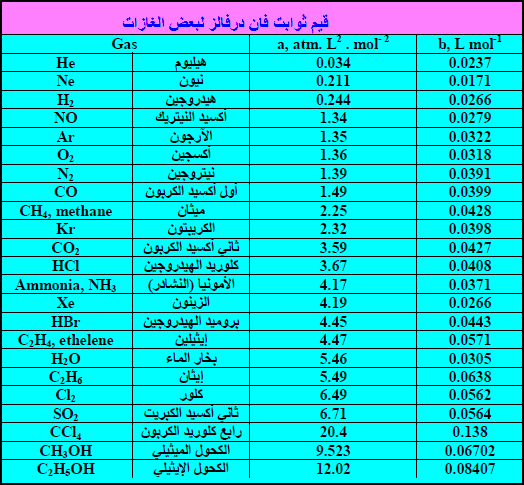
قيم الثوابت (a , b) لمعادلة الحالة لفان در فالز

– إن قیم الثوابت (a, b) تعتمد على طبیعة الغاز لأن الأحجام الجزیئیة والتجاذبات الجزیئیة تتغیر من غاز الى آخر وتعین قیمتھا العددیة من التجارب العملیة.

ملاحظات هامة على قيم (a , b)

(1) قيمة (a) ھي تعبیر عن قوة تجاذب نوع معین من جزیئات الغاز لنوع آخر من الجزیئات. ونلاحظ من الجدول أن قیمة الثابت (a) للهيليوم أقل القيم وبالتالي فلذرات الھیلیوم أضعف تجاذب فیما بینھا.

(2) یلاحظ في الجدول أن الجزیئات المحتویة على ذرات عدیدة مثل وھذا لیس مدعاة للدھشة إذ أنه من المتوقع أن تكون مثل ھذه الجزیئات أكبر من جزیئات تحتوي على بضع ذرات فقط. فمثلاً قیمة الثابت (b) لـ NH₃ أكبر من H₂
لأن جزئ NH₃ يحتوى على أربع ذرات بينما H₂ يحتوى على ذرتين.

(3) التنویع بین قیم (a) بعكس التنويع في شدة الجذب بين الجزيئات. ومن السهل ان نفهم سبب جذب الجزيئات القطبية مثل: C₂H₅OH , CH₃OH , H₂O , NH₃ بعضها البعض. فھذه الجزیئات ثنائیة القطبیة تمیل الى صف نفسھا بحیث أن الشحنة الموجبة الجزئیة على أحدھا تجذب الشحنة السالبة الجزئیة على أخرى. وبالتالي فقیم (a)للجزیئات القطبیة مرتفعة

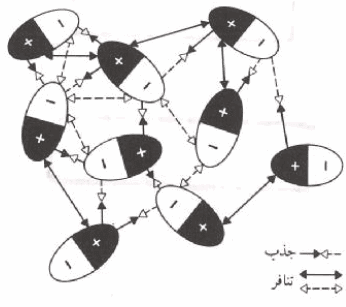
الشكل التالي: التفاعل الإلكتروستاتیكي المتبادل بین ثنائیات القطب. تفوق التجاذبات بقوتھا قوى التنافر، وھكذا تشعر الجزیئات بتجاذب نحو بعضھا البعض.

(4) أما التجاذب بین الجزیئات اللاقطبیة مثل O₂, CH₄, C₂H₆ أو بين ذرات منعزلة مثل He والغازات الكريمة الأخرى فهو أكثر صعوبة في التفسير. إلا أن الجزئيات غير القطبية عموماً مثل (CO₂ , O₂ , N₂) لها قيمة (a)منخفضة لأن التجاذب بین جزیئاتھا منخفض مقارنة بالجزیئات القطبیة.

– يلاحظ أن قيم الغازات الخاملة مثل غاز الهيليوم (He) له قيم (a)منخفضة جداً لأن قوى التجاذب بین جزیئاتھا صغیر جداً. وعموماً فإن قیمة (a) في ھذه الغازات تزداد مع زیادة العدد الذري، بسبب زیادة قوى فان درفالز (لندن) فمثلاً قيمة (a) لـ:

– ومن خلال قیم المناقشة أعلاه لقیم a, b نتمكن من توسیع معرفتنا حول الجزیئات المكونة للغاز الحقیقي.

– ویتم الحصول على ثابتي فان درفالز لغاز ما من تقدیم أفضل تطابق مع المعطیات التجریبیة. ومن ھذا المنطلق فإن كمیات یتم تحدیدھا تجریبیاً وھي تمكننا من فحص نظریاتنا المتعلقة بالأحجام والتجاذبات الجزیئیة.

شرح سلوك الغاز الحقيقي من خلال معادلة فان درفالز

– یمكن لمعادلة فان درفالز أن تشرح سلوك الغازات الحقیقیة الى بعض المدى، ولكن لیس على الإطلاق كما سیرد شرحه فیما یلي.–  معادلة فان درفالز لمول واحد من الغازات (n =1)

وبترتیب المعادلة:

(أ) عند الضغوط المنخفضة:

– عندما تكون P صغيرة فإن V سوف تكون كبيرة. وحينئذ فإن الحدين (Pb , ab/V²) يمكن إهمالها بالمقارنة بالحد a/V . وتكون b أيضاً صغيرة جداً بالمقارنة بالمقدار V . وبذلك تختصر المعادلة:

إلى:

– وبذلك فإنه عندما:

(1) يكون الضغط منخفضاً فإن حاصل ضرب PV يكون أقل من RTبكمية تساوي (a/V)

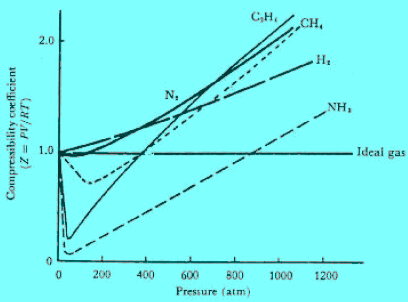
(2) عندما تزداد P فإن V تقل أو (a/V) تزداد. وبذلك فإن PV سوف تستمر في النقص. وهذا يوضح الإنخفاض في منحنى العلاقة بين Z مقابل P بالنسبة لغازات (NH₃ , N₂ , CH₄)

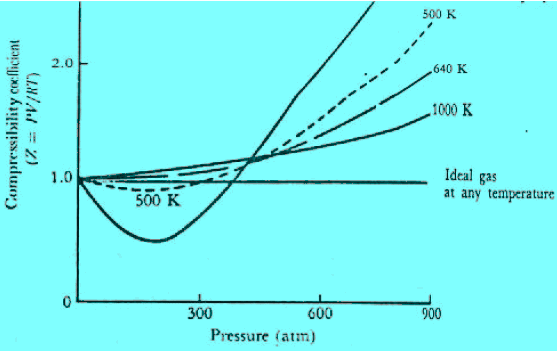
– الشكل التالي : يوضح منحنيات معامل الإنضغاط (PV/RT=Z) مقابل الضغط بالنسبة لعديد من الغازات. ويتضح منها الحيود عن قانون الغاز المثالي بلغة معامل الإنضغاط حيث ينشأ انخفاض عن قيمة Z أقل من (1.0)
نتيجة للتجاذب المتبادل بين الجزيئات في حين ينتج ارتفاع في قيمته (Z = 1.0) نتيجة لقوى التنافر المتبادل بين الجزيئات. إذ تكون الجزيئات ذات الحجم المتناهي في الصغر في حالة تلاصق مزدحم مع بعضها البعض.

(ب) عند الضغوط العالية:

– عندما تكون P عالية في المعادلة:

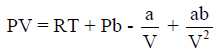
فإن V سوف تكون صغيرة ، ويصبح الحدان (a/V , ab/V²)واللذان لھما إشارتان متضادتان، ولھما تقریباً نفس القیمة، یمكن إھمالھما لصغرھما بالمقارنة بالحدین الآخرین في الجانب الأیمن من المعادلة والتي تختصر الى:

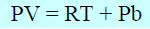
وبذلك فإنه عندما یكون الضغط عالیاً ، فإن حاصل ضرب PV)) يكون أكبر من المقدار (RT) بكمية تساوي (Pb) كما أنه يزداد زيادة خطية بزيادة الضغط.

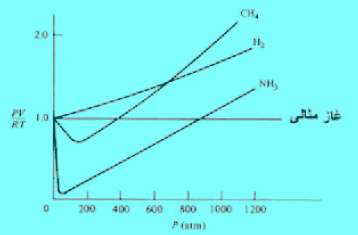
– ویوضح ذلك، لماذا عند ضغوط عالیة، یكون حاصل ضرب (PV) دائماً أكبر من القیمة المتوقعة بالنسبة لجمیع الغازات كما بالشكل التالي:

(جـ) عند ضغوط منخفضة للغاية، ودرجات حرارة عالية:

(1) عندما تكون P صغيرة جداً :
فإن V سوف تكون كبيرة جداً. وفي هذه الحالة: فأن كلاً من (b, a/V²) في معادلة فان درفالز:

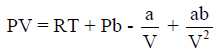
يمكن إهماله لصغره ، بالمقارنة بالحدين V , P ونختصر معادلة فان درفالز إلى العلاقة:

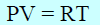
وھي العلاقة الخاصة بالغاز المثالي.

(2) وبالمثل فإنه عندما تكون درجة الحرارة عالیة جداً: 

فإن V تصبح كبيرة جداً (حيث أن الحجم يتناسب طردياً مع درجة الحرارة). كما أن P سوف تكون صغيرة جداً، ومرة ثانية نحصل على العلاقة:

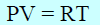
وبذلك ، فإنه عند ضغوط منخفضة ، ودرجات حرارة عالیة، نجد أن جمیع الغازات الحقیقیة تطیع قوانین الغاز المثالي.

السلوك الاستثنائي للهيدروجين والغازات النادرة

– ترجع خصوصیة سلوك غاز الھیدروجین لصغر كتلته مما یؤدي الى إھمال قوى التجاذب بین الجزیئات. وبالتالي یمكن إھمال (a/V , ab/V²) في المعادلة الأساسية لفان درفالز:

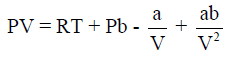
– حیث أن قوى التجاذب المتبادل بین جزیئات ھذه الغازات صغیرة جداً، فقد تبین أن قيم (a)لھذه الغازات صغیرة جداً. وبذلك فإن الحد ((a/V² الذي يكون تأثيره هو الغالب عند ضغط منخفض، یكون صغیراً بحیث یمكن إھماله. ولكن یكون تأثیر المقدار (b)والذي یعبر عن حجم الجزیئات، ھو الغالب، حتى عند ضغوط مختلفة. وبذلك تختصر معادلة فان در فالز الى الصورة:

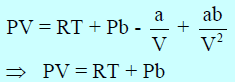
– وبعبارة أخرى یكون حاصل ضرب (PV) بالنسبة لبعض الغازات مثل He , H₂ دائماً أعلى من المقدار RT بكمية تساوي Pb ، وهذا يفسر السبب في أن حاصل ضرب PV بالنسبة لغاز الهيدروجين والهيليوم. وكذلك في الميثان تبدأ في الزيادة الحادة بزيادة الضغط.

– الشكل التالي يوضح منحنى PV/RT بالنسبة لواحد مول من الميثان عند درجات حرارة مختلفة ، ويلاحظ أن قيمة (Z) تكون أقل من (1.0) عند ضغوط منخفضة وتكون أكبر من (1.0) عند ضغوط عالية. ویقترب من سلوك الغاز المثالي عند درجات حرارة عالیة.

– وهكذا نجد أن المقدارين (a/V) ، (Pb) يؤثران في اتجاهين متضادين:

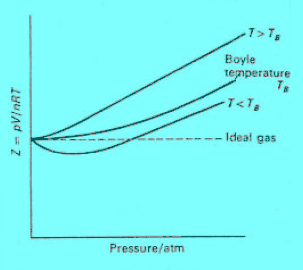
فبينما نجد أن المقدار (a/V) يكون أكثر أهمية عند الضغوط المنخفضة، فأننا نجد أن المقدار (Pb) هو الأكثر أهمية عند الضغوط العالية. وعند ضغوط فيما بين هاتين الحالتين سوف یتزن أحد ھذین العاملین مع الآخر، وحینئذ تتحرك نقطة النھایة الصغرى على المنحنى إلى أعلى متجھة نحو الیسار بارتفاع درجة الحرارة، حتى تقع على خط الغاز المثالي عند درجة حرارة بویل. (كما بالشكل التالي الذي يوضح إيزوثيرمات الغاز الحقيقي موضحة درجة حرارة بويل)

تأثير درجة الحرارة 

– وقد وجد عند درجة حرارة :

(أ) أقل من (-172.8 C^o) : أن منحنى Z – P لغاز الهيدروجين (وأقل من 200 K للميثان) سوف یظھر فیه انحناء بسیط بزیادة الضغط.

(ب) وعند (-164 C^o)(درجة حرارة بويل) (500 K للميثان) يختفى انحناء المنحنى، ویبدأ الھیدروجین (أو المیثان) في السلوك مسلكاً أكثر من مثالي.

– وقد اعتبرت الجزیئات أنھا عبارة عن كرات والتي عندما تكون متراصة الى أقصى حد للإلتصاق. حیث تشغل (% 74) من الحجم المتاح.

–  وإذا كانت (Mw) هو الوزن الجزيئي ، NA عدد أفوجادرو ، (d)هي الكثافة ، فإن حجم الجزئ الواحد Molecular Volume V_m) )

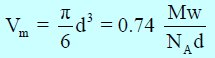
وقيمة (b) للجزئ الواحد (الحجم غير المخترق excluded volume) تساوي:

المراجع:  أسس الكيمياء العامة والفيزيائية – الجزء الأول.عمر بن عبد الله الهزازي ، قسم الكيمياء- كلية العلوم – جامعة أم القرى – المملكة العربية السعودية.