الكيمياء العامة
إيجاد قيم ثوابت معادلة فاندرفالز Van der waal equation Constants

معادلة الحالة لفان در فالزvan der Waals Equation of State
– معادلة فاندرفالز هي معادلة سميت باسم واضعها العالم الهولندي يوهانس ديديريك فان دير فالس وهي معادلة الحالة تقريبية تصف حالة الغازات الحقيقية. تأخذ معادلة فان دير فالس في اعتبارها اختلاف الغاز الحقيقي عن الغاز المثالي .
– العلاقة التالية (القانون العام للغازات):
– العلاقة التالية (القانون العام للغازات):
P V = n R T
لا تكون صحیحة إلا في الحالة المثالیة للغاز، أما في حالة الغاز الحقیقي (الغاز الذي یحید عن السلوك المثالي) فإنھا لا تكون صحیحة (خاصة تحت ضغط عال ودرجة حرارة منخفضة) إلا بعد أخذ تصحیحات فان در فالز في الإعتبار
– إحدى طرق تحسین الدقة ھي تعدیل قانون الغاز المثالي بحیث تؤخذ في الإعتبار العوامل التي تسبب في جعل الغاز الحقیقي مختلفاً (یحید) عن الغاز المثالي.

وبالتعویض بھا في معادلة الغاز المثالي:
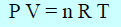
یعطینا:
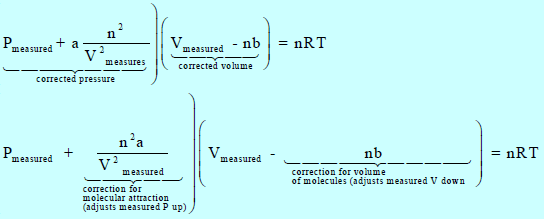
وباختصار فإن المعادلة النھائیة:
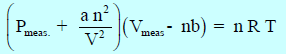
وتعرف ھذه المعادلة بـ معادلة فان درفالز للغاز الحقیقي Van der Waals Equation of State for A real Gas
حيث (a, b): ثابتا فان درفالز، ویعتمدان في قیمتھما على نوع الغاز وعلى الوحدات المستخدمة لقیاس الحجم والضغط، ویتم إیجاد قیمتھما تجریبیاً.
حيث (a, b): ثابتا فان درفالز، ویعتمدان في قیمتھما على نوع الغاز وعلى الوحدات المستخدمة لقیاس الحجم والضغط، ویتم إیجاد قیمتھما تجریبیاً.
إيجاد قيم ثوابت معادلة فاندرفالز للغازات الحقيقية (a,b)
لإيجاد كل من (a) , (b) في معادلة فاندرفالز نتبع الأسلوب التالي:
بضرب معادلة فان درفالز لمول واحد من الغاز:
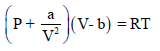
بـــ V2 ينتج:
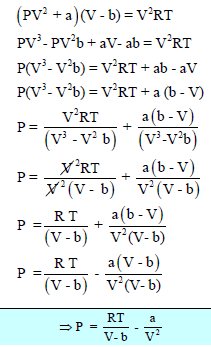
وعند أخذ مشتقة المعادلة الأخيرة بالنسبة للحجم في حالة ثبوت درجة الحرارة فإن:
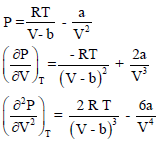
وعندما تكون درجة الحرارة عبارة عن درجة الحرارة الحرجة فإن كل من المشتقة الأولى والثانية للضغط بالنسبة للحجم تساوي صفراً لأن مشتقة الثابت تساوي صفراً.
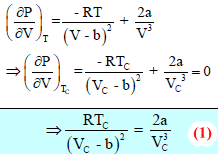
وإن:
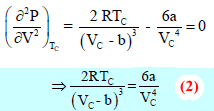
وبقسمة المعادلة (1) على المعادلة (2) ينتج:
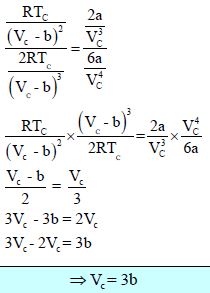
وبالتعويض عن (Vc) من المعادلة Vc = 3b في المعادلة (1) ينتج:
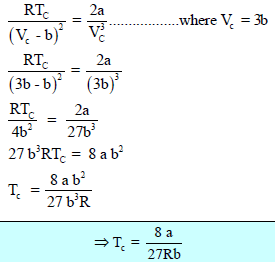
ومن معادلة فاندرفال:
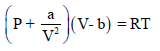
فأن:
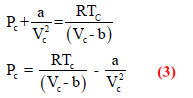
وبالتعويض في المعادلة (3) عن قيم (Tc , Vc) من المعادلتين:
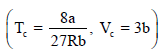
ينتج:
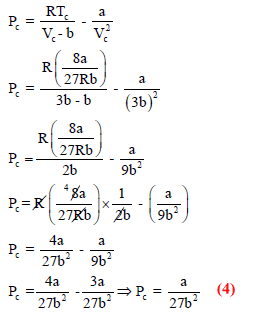
وإن النسبة بین درجة الحرارة الحرجة والضغط الحرج ھي:
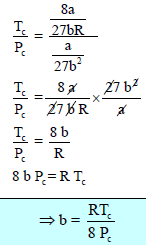
وبالتعويض عن (b) بالمعادلة (4) ينتج:
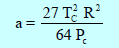
من هذا يتضح أن لــ (a) قيمة ثابتة لا تعتمد على الضغط ودرجة الحرارة وأنهما مقیاس لقیمة قوى التجاذب الموجودة بین الجزیئات.
ملاحظات هامة
– عند تطبیق المعادلة:
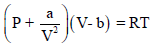
یجب اختیار الوحدات الملائمة لكل من (a) , (b) بحيث تتناسب مع وحدات الضغط والحجم وثابت الغاز.
– عند وجود عدد (n) من المولات فإن المعادلة تؤول إلى:
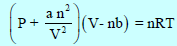
– فى المسائل الحسابية نقوم أولاً بحساب الضغط (P) ويسبقه حساب الثوابت (a , b) من المعادلات:
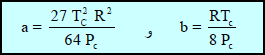
مسائل محلولة
مثال (1): أرید حساب ضغط الأمونیا (NH3) المتولد من مولين (2 moles) والذي يشغل حجماً مقداره (5 L) وعند درجة حرارة (27Co).
الحل:
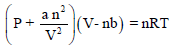
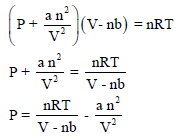
** من جدول الظروف الحرجة للغازات نجد أن الظروف الحرجة لغاز الأمونيا هي:
Pc
= 111 atm , Tc = 406 K
= 111 atm , Tc = 406 K
ومن ھنا نستعمل الوحدات العالمیة حیث تكون وحدات الضغط بــ N/m2 وإن:
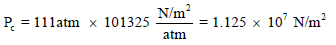
والحجم بوحدة المتر المكعب:
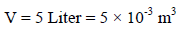
** لإيجاد قيم كل من (a , b) نعوض في المعادلتين:

** أما في حالة استعمال معادلة الغاز المثالي:
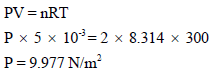
وھذا یدل على انخفاض الضغط في حالة الغاز الحقیقي نتیجة لقوى التجاذب الموجودة بین جزیئات الغاز.
مثال (2):
(أ) باستعمال معادلة فان در فالز، احسب الضغط المسلط على (100 g) من غاز أول أكسيد الكربون (CO)
الموجود في إناء حجمه (5 L) وفي درجة حرارة (40 Co).
(ب) قارن تلك القيمة بالفقرة (أ) مع القيمة المحسوبة في حالة كون الغاز مثالياً.
علماً بأن الكتل الذرية (C =12 , O = 16)
الحل:
(أ) باستعمال معادلة فان درفالز للغاز الحقیقي فإن:
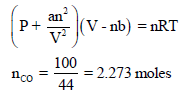
ولحساب الثابتين (a , b) فإن:
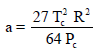
وقیم الظروف الحرجة لغاز أول أكسيد الكربون یمكن استخراجھا من جدول الظروف الحرجة للغازات فإن:
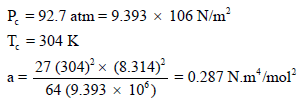
وبتطبیق معادلة فان درفالز:
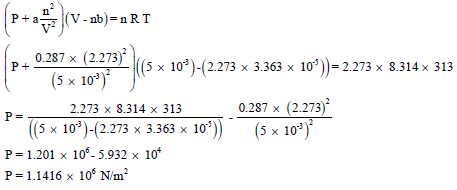
(ب) باستعمال معادلة الغاز المثالي:
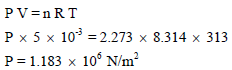
أي أن الضغط المثالي أكبر من الضغط الحقیقي بمقدار(0.0414 × 106 N/m2) لأنه في الحالة المثالیة یفترض أن الغاز في حالة عشوائیة كاملة ولا وجود لقوى التجاذب بین جزیئاته لذا كان مقدار التصادمات لجزیئاته على الجدار الداخلي للإناء عالي مما یسبب زیادة الضغط. أما بالنسبة للغاز الحقیقي فإن قوى الترابط بین جزیئاته موجودة بالرغم من ضعفھا مما تعرقل حركة الجزیئات بعض الشيء وبالتالي انخفاضاً في عدد التصادمات لجزیئاته على الجدار الداخلي للإناء الموجود فیه الغاز.
المراجع: أسس الكيمياء العامة والفيزيائية – الجزء الأول.عمر بن عبد الله الهزازي ، قسم الكيمياء- كلية العلوم – جامعة أم القرى – المملكة العربية السعودية.







اريد ايجاد قيمة نسبةNa2O من خلال جدول التحليل الكيميائي للاكاسيد المكونة للصخور الناري بطريقة التحليل الطيف المرئي
حيث اجري التحليل للصخر الناري وكان اكسيد الصوديوم مفقود القيمة في الجدول الموضح لنتائج الاكاسيد فما هي المعادله الرياضيه التي يمكن تطبيقها في مثل هذه الحالة لايجلإ قيمه اكسيد الصوديوم دون الرجوع إلى التحليل مرة أخرى
كيفية ايجاد معامل التمددية من معادلة فان دير فالز ؟