الكيمياء العامة
قانون جراهام للتدفق والانتشار Graham’s Law of Diffusion and Effusion

أولاً/ الفرق بين التدفق (Effusion) والانتشار (Diffusion)
– یلزم التفریق بین مصطلحین ھما الإنتشار (Diffusion) والتدفق (الإنبجاس) .(Effusion)
– من النتائج لحركة الغازات الدائمة العشوائية وسرعتها العالیة أن الغازات تختلط بسرعة عالیة عندما تكون على اتصال أو خلال وعاء.
– تختلف عملية الانتشار(Diffusion) عن عملية التدفق (Effusion) حيث تدل عملیة الانتشار على انتشار غاز مع غاز آخر. أما التدفق فیدل على اندفاع الغاز من خلال فتحة ضیقة.
ثانياً/ انتشار الغازات Gas Diffusion
سنتناول هذه العملية في النقاط الآتية:
(1) یطلق عمليات الانتشارعلى مرور الغاز مثلاً من خلال مادة مسامیة بحیث یكون الضغط واحداً على جانبي ھذه المادة.
(2) كما تطلق عملیات الإنتشار على تحرك جزیئات الغاز لتحتل الحیز المتاح لھا (میل المادة للتمدد وبانتظام وخلال الفضاء المسموح به فقط).
(3) تعريف الانتشار في الغازات Diffusion :
ھو الخلط التدریجي لجزیئات أحد الغازات مع جزیئات غاز آخر (العملیة التي یختلط بھا أحد الغازات تدریجیاً مع غاز آخر) نتیجة لخواصھا الحركیة،
(4) مثالاً مباشراً لذلك هي الحركة العشوائیة للغازات حیث تتحرك جزیئات أحد الغازین بحریة في الفراغات الموجودة بین جزيئات الغاز الآخر. وبذلك یمكن القول بأن أي غاز یكون تام الذوبان في أي غاز آخر.
(5) تعريف مصطلح الانتشار باللغة الأنجليزية:
Mixing of different gases by random molecular motion with frequent collisions is called diffusion
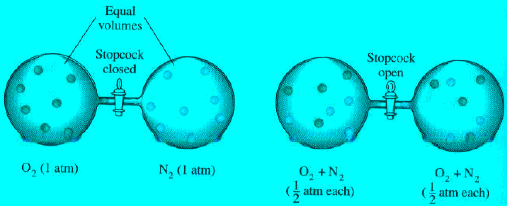
(6) تحدث ھذة الظاھرة بسرعة كبیرة في الغازات في حین تكون بطیئة جداً في المواد الصلبة. فالغازات تنتشر لتملأ كل الإناء الذي یشغله الغاز وفي كل الإتجاھات وحتى ضد الجاذبیة. ویمكن ملاحظة ذلك عندما نرش كمیة من العطر، فسرعان ما تملأ رائحتھا الغرفة. وقد وجد أن الغاز الذي وزنه الجزیئي صغیر (خفیف الوزن) ھو الأسرع انتشاراً. ویمكن ملاحظة الإنتشار بسھولة من الأمثلة التالیة:
(أ) عند إطلاق بعضاً من الأمونیا (النشادر) NH3 إذ سرعان ما تملأ رائحتها الغرفة، مما یعني أن الأمونیا قد أصبحت موزعة في كل مكان من الحجم الكلي للحجرة.
(ب) عند نزع غطاء قارورة عطر فإن الرائحة ستنتشر بسرعة خلال الغرفة. كلما اختلطت جزیئات العطر بجزیئات الھواء. ھذا الخلط لغازات مختلفة بواسطة الحركة الجزیئیة العشوائیة (Random Molecular Motion) بتصادمات متكررة یسمى الإنتشار(diffusion).
(جـ) كبریتید الھیدروجین H2S (رائحة البیض الفاسد) إذا حرر في غرفة كبیرة، فإن الرائحة بعد زمن یسیر یمكن تمییزھا خلال الغرفة.
السرعات الجزیئیة للغازات
(7) بالرغم من أن السرعات الجزیئیة للغازات كبیرة جداً إلا أن عملیة الإنتشار نفسھا تأخذ وقتاً طویلاً نسبیاً لكي تكتمل. فمثلاً عند فتح قارورة ملیئة بمحلول الأمونیا المركز NH3 عند أحد أطراف طاولة بالمعمل فیجب أن یمر بعض الوقت قبل أن یشم شخص آخر رائحة الأمونیا عند الطرف الآخر للطاولة . والسبب في ذلك یكمن في أن الجزیئات تتعرض لعدد كبیر من التصادمات في طریقھا من أحد أطراف الطاولة الى الطرف الآخر.
(8) إذاً یحدث انتشار الغازات تدریجیاً ببطء (gradually) ولیس لحظیاً .(instantly)وھو الشيء الذي یبدو متوقعاً من السرعات الجزیئیة العالیة. وإضافة الى ذلك، فنجد أن الغاز الأخف (الذي وزنه الجزیئي صغیر) ینتشر عبر حیز معین أسرع من الغاز الأثقل وذلك بسبب أن الجذر التربیعي لمتوسط سرعة الغاز الخفیف تكون أكبر من سرعة الغاز الثقیل.
(9) جزیئات الغاز تتحرك بسرعة كبیرة جداً. لكن یجب أن یؤخذ بعین الإعتبار أن متوسط المسافة التي یقطعھا أي جزيء بین تصادمین صغیراً جداً. وبذلك، فإن الإنتشار في فراغ سوف یحدث بسرعة أكبر بكثیر من الإنتشار في غاز آخر. إذ أن المعدلات النسبیة لانتشار غازین في ثالث (أو في فراغ) تعتمد على طبیعة الغازین المعنیین.
ثالثاً/ تدفق الغازات (الإنبجاس) Gas Diffusion
(1) التدفق ھو عملیة مرور غاز (تحركه وتمدده) وتسربه تحت الضغط ، من فتحة صغیرة جداً (ثقب ضیق) أو خلال أنابیب ضیقة جداً أو مادة مسامیة في جدار الوعاء الذي یحوي ھذا الغاز، من منطقة ذات ضغط مرتفع الى منطقة ذات ضغط أقل على جانبي المادة المسامیة.
(2) تعريف التدفق (Effusion):
ھو العملية التي تمكن أحد الغازات الذي یكون تحت ضغط ما بالھروب من إحدى حجرات الإناء الى الأخرى عبر ثقب صغیر. كما أن التدفق یمثل العملیة التي فیھا جزیئات الغاز تھرب بدون تصادمات خلال فتحة صغیرة جداً الى الفراغ.
(3) تعريف مصطلح معدل التدفق باللغة الأنجليزية:
The rate of effusion is the number of molecules passing through a porous hole in a given time
(4) إذا كان ذلك الثقب في أحد جوانب الوعاء الحاوي صغیراً لدرجة كافیة (یجب أن یكون قطر الثقب صغیراً بالمقارنة بمتوسط الممر الحر للغاز) فإن الجزيء المنطلق نحو الإصطدام بجدار الإناء الحاوي سوف یلاقي فرصة الخروج عبر الثقب الى الغاز الموجود في الخارج.
(5) الشكل التالي توضح تدفق أحد الغازات في الفراغ.
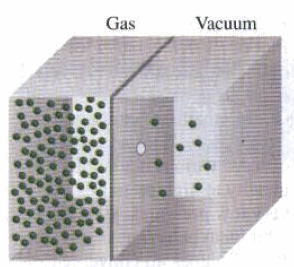
(6) يبين الشكل السابق اندفاق الغاز من فتحة ضیقة في جدار الوعاء الحاوي. وھو احتمال استنبطه جراھام بالنسبة لجزیئات تصطدم بجدران الوعاء الحاوي. وقد أعلن بأن معدل تسرب الغاز خلال فتحة ضیقة، یتناسب عكسیاً مع الجذر التربیعي لوزنه الجزیئي، أو یتناسب طردیاً مع سرعة جزیئاته طبقاً للنظریة الحركیة.
(7) ظاھرة التدفق ھذه مسؤولة عن انكماش بالون الأطفال المملوء بغاز الھیلیوم. حیث یمكن للغاز وھو مكون من ذرات He صغیرة جداً أن یتدفق خلال المسامات الصغیرة جداً الموجودة في مادة المطاط الرقیق المصنوع منھا البالون. ولو كان مملوءاً بالھواء لكان تسربه أكثر بطئاً من غاز الھیلیوم.
(8) یعتبر معدل تدفق غاز(انبجاسه)، تحت ظروف قیاسیة من الخواص الممیزة للغاز.
(9) نظراً لأنه من الصعب نظریاً وعملیاً أن نتعامل مع القیم المطلقة لمعدلات الإنبجاس (التدفق) من خلال ثقب ذي أبعاد محددة لذلك اكتفي باستخدام المعدلات النسبیة لانبجاس الغازات.
(10) بالرغم من أن التدفق یختلف عن الإنتشار في طبیعته إلا أن معدل التدفق في الغازات یعطى أیضاً بقانون جراھام للإنتشار مثلما ھو الحال بالنسبة للإنتشار فإننا نرى عند درجة الحرارة المعینة، أن الغازات الخفیفة تتدفق أسرع من الغازات الثقیلة.
رابعاً/ معدل التدفق rate of effusion
– معدل التدفق rate of effusion:
عبارة عن عدد الجزیئات المارة خلال ثقب مسامي في زمن معطى.
– تعريف مصطلح معدل التدفق باللغة الأنجليزية:
The rate of effusion: is the number of molecules passing through a porous hole in a given time.
– ويمكن التعبير عنه بالعلاقة الآتية:
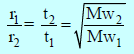
The longer the time it takes, the slower is the rate of effusion
– وقد درس العالم الكیمیائي البریطاني (توماس جراھام Thomas Graham ) في عام ١٨٢٩ م معدلات التدفق للغاز المختلفة. وأجرى قیاسات على الإنبجاس النسبي لعدد كبیر من الغازات. ووجد أنه عندما تكون ھذه الغازات تحت نفس الظروف من الضغط ودرجة الحرارة (ثبوت درجة الحرارة وثبوت فرق الضغط) فإن معدل تدفقھا من فتحة صغیرة في الجدار یتناسب عكسیاً مع الجذر التربیعي للكثافة لھذه الغازات:
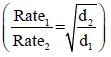
وھذا ما یسمى بقانون جراھام.
ولقد نتجت ھذه العلاقة عندما قیست سرعات الإنبجاس بدلالة حجم الغاز المنبجس في الثانیة تحت درجة حرارة معینة وضغط معین
خامساً/ قانون جراهام للتدفق والانتشار
– ینص قانون جراھام للإنتشار أو التدفق Graham’s Law of Diffusion and Effusion of Gases على:
(أن معدل انتشار غاز ما یتناسب عكسیاً مع الجذر التربیعي لكثافته وذلك عنددرجة حرارة معینة)
– عند ضغط ثابت فإن:
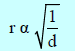
حيث r: معدل انتشار الغاز. وھذا ما یعرف بقانون جراھام للإنتشار.
– وإذا افترضنا معدلین للإنتشارr1 , r2 ذاتى كثافة d1,d2 على الترتيب فإن:
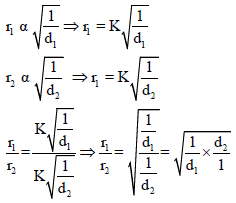
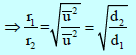
– من العلاقة :
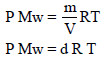
نلاحظ أن الكثافة تتناسب طردیاً مع الوزن الجزیئي:
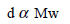
لذلك :
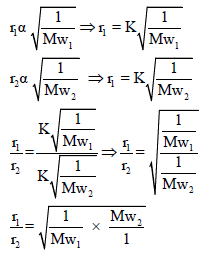
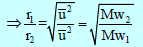
– طبقاً لفرض أفوجادرو تتناسب كثافة الغاز تناسباً طردیاً مع وزنه الجزیئي فإن ملاحظة جراھام تتفق مع النظریة الحركیة التي تتنبأ بأن معدل تسرب الغاز یتناسب طردیاً مع السرعة الجزیئیة أو یتناسب عكسیاً مع الجذر التربیعي للوزن الجزیئي.
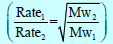
– وإذا أخذنا في الإعتبار الزمن اللازم للتدفق (t) فیمكن أن نكتب العلاقة لتدفق الغازات كالآتي :
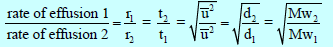
– ویصعب عملیاً مقارنة المعدلات النسبیة لانتشار غازین عند نفس الظروف من درجة الحرارة والضغط. ولكن من الأسھل مقارنة المعدلات النسبیة لتدفق الغازین.
سادساً/ الحيود عن قانون جراهام للتدفق والانتشار
(1) وجد أن الحیود عن ھذا القانون یحدث عند ضغوط عالیة. حیث تتصادم الجزیئات عدة مرات مع بعضھا البعض أثناء تسربھا عبر الثقب.
(2) بمقارنة النتائج العملیة مع تلك المحسوبة من النظریة الحركیة أوضحت اتفاقاً كبیراً عندما كان ضغط الغاز منخفضاً وأن حجم الثقب الذي یحدث اندفاق الغاز خلاله صغیراً. وعند الضغوط المنخفضة یكون متوسط الممر الحر للغاز كبیراً لدرجة كافیة، وبذلك تكون إمكانیة حدوث التصادم الجزیئي في منطقة الثقب أقل منھا عند ضغوط أعلى. وبالمثل، فإنه إذا كان قطر الثقب كبیراً نسبیاً، فإنه سوف یصبح للجزیئات فرصة أكبر للإصطدام مع بعضھا البعض عند المرور عبر الثقب، وسوف لا تصبح الإفتراضات الأساسیة قائمة.
(3) یفشل قانون جراھام أیضاً إذا كانت الثقوب كبیرة لدرجة كافیة بحیث یسمح بتدفق ھیدرودینامیكي للغاز بقوة نحو الثقب (مثل انبثاق الماء) ولكن مادامت الجزیئات المعزولة عن بعضھا البعض تتسرب عن طریق سیرھا عبر الفتحة أثناء تحركھا العشوائي خلال غاز مستقر، فإن الإفتراضات من النظریة الحركیة الجزیئیة سوف تنطبق.
سابعاً/ التطبيقات الهامة لقانون جراهام للإنتشار
(1) التطبيق الأول: تعیین كثافة الغازات، وأوزانھا الجزیئیة
– إذا سمح لغازین (A, B) بالتدفق عند نفس الظروف من درجة الحرارة، والضغط، وذلك عبر نفس الفتحة، في تجربتین منفصلتین فإن:
– عادة ما تجرى التجربة بالسماح لنفس الحجم من كل غاز بأن یتدفق عند نفس الظروف من درجة الحرارة، والضغط، وملاحظة الزمن الذي یستغرقه كل غاز في الإندفاق . وحیث أنه یمكن اعتبار الأزمنة بأنها تتناسب عكسیاً مع معدلات الإندفاق فإن:
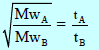
حيث (tA, tB) الزمن الذي یستغرقھ حجم معین من الغاز A, B لكي یتدفق.
وإذا عرف الوزن الجزیئي لأحد الغازین، فإنھ یمكن حساب الوزن الجزیئي للغاز الآخر.
(2) التطبيق الثاني: الفصل الفیزیائي للغازات
– یشمل التطبیق الثاني للتدفق الغازي على الفصل الفیزیائي للغازات (فصل مخالیط الغازات عن بعضھا) التي یصعب فصلھا بطریقة أخرى، ومن ذلك فصل مخالیط النظائر المشعة (نظائر الیورانیوم U) (یورانیوم ٢٣٥ ، یورانیوم ٢٣٨) لتحضیر وقود الأفران الذریة نظراً لأھمیة العنصر الأول وقابلیته للإنشطار.
– یحتوي خام الیورانیوم (الخام الأساسي یسمى بتشبلند (Pitchblendeعلى نظیر اليورانيوم 238 بنسبة99.28% وعلي نظير اليورانيوم الأهم وهو يوارنيوم 235 بنسبة 0.71% والنظير يورانيوم 238ھو القابل للإنشطار النووي ویستخدم في محطات القوى النوویة وفي الأسلحة النوویة.
– من طرق فصل ھذین النظیرین يورانيوم 238 عن يورانيوم 235 ھو استخدام كمیات كبیرة من غاز الفلور F2)) للحصول على سادس فلورید الیورانیوم UF6 ، وعند السماح لغاز سادس فلورید الیورانیوم بالإنتشار ببطء، فإنه نظراً للفرق في الوزن الجزیئي للنظیرین يكون معدل الإنتشار مختلفاً ویمكن فصل النظیرین بھذه الطریقة.
– وبالرغم من أن الفرق في الأوزان الجزیئیة النسبیة صغیر ( 1.0043 ). إلا أن تكرار عملیة التدفق خلال حواجز منفذة (یقدر عددھا بالآلاف) تحتوي على ثقوب صغیرة جداً. یؤدي الى جعل الخلیط غنیاً في حالته النھائیة بالفلورید الطیار UF6 ( لليورانيوم 235) القابل للإنشطار وبالتالي یمكن الحصول على وفرة جوھریة من النظیر 235 المرغوب فیه.
(3) التطبيق الثالث: في مجال الطب
ھناك تطبیق للتدفق الغازي في مجال الطب. حیث تستبدل مخالیط الأكسجین، والھیلیوم بدلاً من الھواء العادي. وذلك للمساعدة على التخلص من الصعوبات المتعلقة بالتنفس. إذ أن المرضى یتنفسون بسھولة أكبر نظراً للمعدل الأكبر لانتشار الھیلیوم بالمقارنة بالنیتروجین الموجود في الھواء العادي.
المراجع: أسس الكيمياء العامة والفيزيائية- الجزء الأول.عمر بن عبد الله الهزازي ، قسم الكيمياء- كلية العلوم – جامعة أم القرى – المملكة العربية السعودية