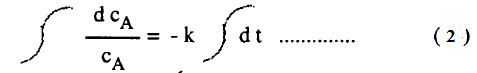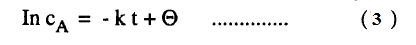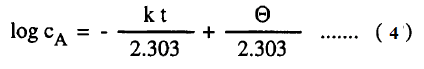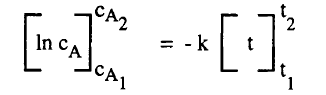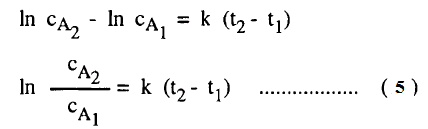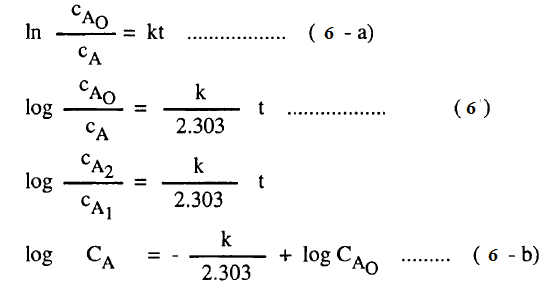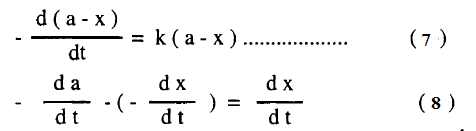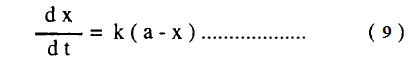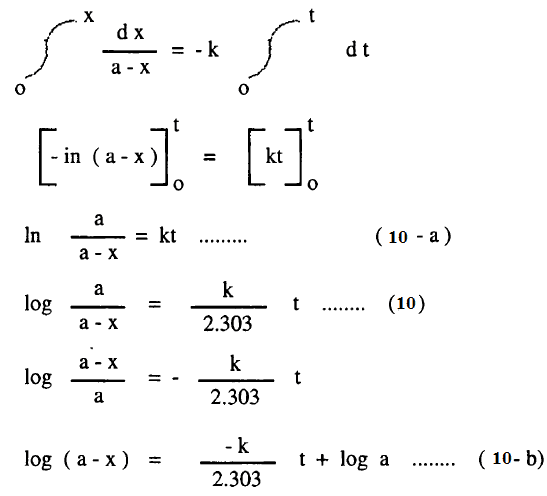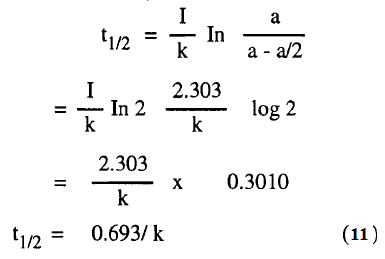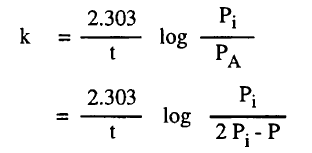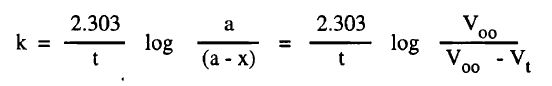تفاعلات الرتبة الأولى First Order Reactions
محتويات الموضوع
تعريف تفاعلات الرتبة الأولى First Order Reactions
– تفاعلات الرتبة الأولى هي التفاعلات التي تعتمد فيها سرعة التفاعل على تركيز مادة متفاعلة واحدة فقط ويمثل التفاعل بالمعادلة العامة التالية:
A → Products
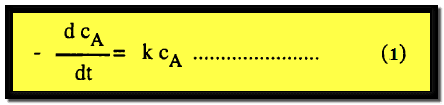
حيث تتناسب سرعة التفاعل مع تركيز المادة (A) مرفوعاً إلى أس واحد، وتكتب المعادلة الرياضية التي تمثل معدل اختفاء المادة (A) مع الزمن كالآتي:
ثابت سرعة التفاعل من الرتبة الأولى K
– يسمى K فى المعادلة السابقة ثابت السرعة للتفاعل من الرتبة الأولى. وهو يساوي سرعة التفاعل عندما يكون التركيز مساوياً للوحدة.
– وحيث أن قيم كل من dcA/dt ، cA لها وحدات تركيز/زمن ، تركيز على التوالي فأن وحدة ثابت السرعة تكون مقلوب الزمن (زمن-1)
K = – (dcA/dt) / cA
= (concentration/time) / concentration
= 1 / time = time-1
– بالنسبة لتفاعلات الرتبة الأولى تكون K ثابت مميز للتفاعل ولا تعتمد على وحدات التركيز المستعملة.
استنتاج المعادلة الحركية لتفاعلات الرتبة الأولي
الطريقة الأولي
– للحصول على تعبير يربط العلاقة بين تركيز المادة المتفاعلة والزمن يجب إجراء التكامل للمعادلة (1) والذي يتم بضرب الطرفين في dt/cA
– وتسمي هذه العملية بفصل المتغير لأن كلاً من طرفي المعادلة (2) يحتوي على دوال لمتغير واحد وبإجراء التكامل:
– حيث Ɵ هي ثابت التكامل وباستعمال اللوغاريتمات للأساس (10) نحصل على :
– وتعطي المعادلة (4) تركيز المادة عند زمن معين t ويمكن استبعاد ثابث التكامل إذا أجرينا التكامل بين الحدود cA1 عند زمن t1 ، cA2 عند زمن t2 أى أن تركيز A عند t1 يكون cA1 وعند t2 يكون cA2 ويعطى التكامل المعادلة الآتية:
– ويمكن تمثيل التركيز cA1 عند زمن t1 بالتركيز الابتدائي cA0 عند زمن t = 0 وكذلك التركيز cA2 بالقيمة CA المتبقية عند زمن t2 = t ، وتصبح المعادلة (5) كالآتي:
الطريقة الثانية
– ويمكن التعبير عن قانون السرعة بطريقة أخرى كالتالي:
– إذا كانت a هي التركيز الابتدائي للمادة A ، X تركيز المادة المستهلكة عند زمن t فإن (a-x) تمثل تركيز المادة A بعد زمن t
وبالتعويض فى المعادلة (1) فإن:
– وذلك لأن da/dt تساوي صفراً حيث أن a ثابت ومن المعادلات (7) ، (8) نحصل على:
– فى المعادلة (9) يلاحظ أن dx/dt كمية موجبة لأن X تزداد مع الزمن
– يفصل المتغيرات ثم إجراء التكامل للمعادلة (9) عند X=0 عند زمن t=0 ، X=X عند زمن t
– المعادلات (10 – a) ، (10) ، (10-b) تمثل كل منها المعادلة الحركية للتفاعل من الرتبة الأولي.
– ويلاحظ أن المعادلات (18 – a) ، (18 – b) مطابقة تماماً للمعادلات (14 – b) ، (14 – a) على التوالي حيث أن a = cAo ، (a-x) = cA
العلاقة البيانية لتفاعلات الرتبة الأولي
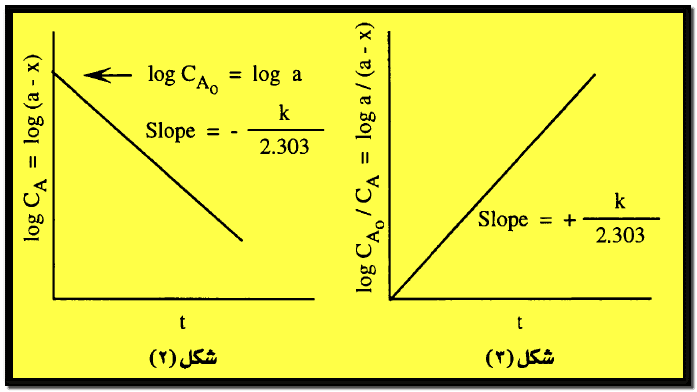
– يتضح من المعادلات (6 -b) ،(10 -a) أن العلاقة البيانية log cA أو log (a-x) والزمن تعطي خطاً مستقيماً له ميل سالب يساوي – K/2.303 أي أن K يمكن الحصول عليها من المعادلة:
K = – 2.303 × Slope
– يعطي تقاطع هذا الخط مع المحور العادي (عند t=0) التركيز الأولي للمادة A أي CA0 أو a كما هو مبين في الشكل رقم (2).
– أي أنه للتعيين إذا كان التفاعل من الرتبة الأولي أم لا ترسم العلاقة بين log CA والزمن فإذا نتج خط مستقيم يمكن أن يكون التفاعل من الرتبة الأولي.
– ويستنتج من المعادلات (6) ، (10) أن رسم العلاقة بين log CA0/CA أو log a/(a-x) مع الزمن يعطى خطاً مستقيماً له ميل موجب يمر بنقطة الأصل ويساوي هذا الميل K/2.303 كما يتضح في الشكل رقم (3).
فترة نصف العمر Half Life period
– تعرف فترة نصف العمر لأي تفاعل بأنها الزمن اللازم لكي ينخفض تركيز المادة المتفاعلة إلى نصف قيمته الأولية أو الزمن اللازم لإتمام نصف التفاعل
– أي عندما تصبح x = a/2 وبالتالي عندما تصبح القيمة المتبقية (a-x) تساوي a/2.
– بالتعويض عن x بالقيمة a/2 وعند t بالقيمة t1/2 فى المعادلة (10) نحصل علي:
– ومن الواضح أن هذا التعبير لا يحتوي على a أي فترة نصف العمر لأي تفاعل من الدرجة الأولى لا تعتمد على التركيز الأولى يستغرق نفس الزمن لإتمام نصف التفاعل مهما كانت قيمة التركيز الأولى كبيرة أو صغيرة.
أمثلة لتفاعلات الرتبة الأولي
(أ) تفاعلات غازية من الرتبة الأولى
– ومن أمثلتها التحلل الحراري لأكسيد النيتريك وخامس أكسيد النتيروجين والأثيرات الأليفاتية ومركبات الآزو والأمينات وبروميد الإيثيل.
– وفيما يلي شرح لبعض هذه التفاعلات كما يلي:
(1) التحلل الحراري للأزوأيزوبروبان Azoisopropane
يتحلل هذا المركب إلى الهسكان والنتروجين طبقاً للمعادلة:
(CH3)2CHN = NCH(CH3)2 → N2 + C6H14
بين درجات الحرارة 250 ، 290 مo وتدرس سرعة التفاعل بقياسات الضغط والمعلومات الضرورية هنا هي الضغط الأولى للمادة المتفاعلة والضغط الكلى للنظام عند مراحل التحلل المختلفة ويمكن حساب ثابت السرعة كالآتي:
نفرض أن Pi هي الضغط الأولي للمادة المتفاعلة ، P هي الضغط الكلي ، PA هي ضغط المادة المتفاعلة. x هي النقص في ضغط المادة المتفاعلة وكلها عند زمن t وعلى هذا فإن عند كل مرحلة من التفاعل :
PA = Pi – x
, PN2 = PC6H14 = x
ويكون الضغط الكلي للنظام كما يلي:
P = PA + PN2 + PC6H14
= (Pi – x) + x + x
= Pi + x
ومن هذة المعادلة نجد ان:
x = P – Pi
وبالتعويض فى هذه القيمة عن x نحصل علىالمعادلات الآتية كما يلي:
PA = Pi – x = Pi –
( P – Pi) = 2Pi – P
وحيث أن a في المعادلة (10 – a) تتناسب مع Pi ، كذلك (a-x) تتناسب مع PA يكون التعبير عن السرعة كما يلي:
(2) تحلل خامس أكسيد النيتروجين
N2O5 (g) → N2O4 (g) + 1/2 O2 (g)
الضغط الجزئ لخامس أكسيد النيتروجين المتحلل (x) = ضعف الضغط الجزئي للأكسجين المتكون عند أي وقت معين. ومع ملاحظة التعقيد الناتج من تحلل رابع أكسيد النتروجين المتكون كما يلي:
N2O4 → 2 NO2
يمكن حساب الضغط الجزئي للأكسجين من الضغط الكلي للنظام أثناء سير التفاعل. وبتطبيق المعادلة (10) يتضح أن ثابت السرعة لا تتغير قيمته تقريباً في الأزمنة المختلفة وهذا يثبت أن التفاعل من الرتبة الأولى.
(ب) تفاعلات الرتبة الأولى من المحاليل
– هذه التفاعلات مثل تحلل خامس أكسيد النتيروجين في وجود رابع كلوريد الكربون كمذيب وتحلل حمض المالونيك وثلاثي كلورو الخليك في المحاليل المائية وكذلك تفكك أملاح الديازونيوم في الماء.
– وفيما يلي سنورد شرحاً لبعض هذة التفاعلات كما يلي:
(1) تحلل البنزين ديازونيوم كلوريد فى الماء Benzene Diazonium Chloride
– هذا المركب C6H5N = NCl يوجد فقط في المحاليل المائية ويتحلل بالتسخين معطياً غاز النيتروجين.
– ويؤخذ حجم النيتروجين المتكون كمقياس للنقص في تركيز المركب.
يسخن محلول من هذا الملح بسرعة إلى الدرجة المطلوبة ثم يسمح للتفاعل أن يتم في حمام ذي درجة حرارة ثابتة.
– يدرس التفاعل بقياس حجم النيتروجين الناتج (V) بعد فترات زمنية مختلفة ولاستكمال النتائج المطلوبة بحسب التركيز الأولى (معبراً عنه بالسنتيمتر المكعب من غاز النيتروجين ويرمز إليه بالرمز (V0) من كمية المادة الأصلية.
– ويحسب ثابت السرعة كالأتي:
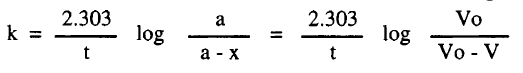
– يحسب ثابت السرعة من ميل الخط المستقيم من رسم log (V0 -V) مع الزمن وعند درجة حرارة 50Co وكمية من المادة المتفاعلة تكافئ 58.3 سنتيمتر مكعب من النيتروجين تكون القيمة كالآتي:
K = – 2.303 × Slope
= – 2.303 × – 0.0303
= 0.0709 min-1
(2) تحلل خامس أكسيد النيتروجين في رابع كلوريد الكربون كمذيب
N2O5 → 2NO2 + 1/2 O2
– يذوب كل من خامس أكسيد النيتروجين وفوق أكسيد النتروجين في رابع كلوريد الكربون ويستقرا في المحلول بينما غاز الأكسجين الذي لا يذوب في هذا الوسط.
– ويقاس حجم الأكسجين المتكون عند فترات زمنية مختلفة ويؤخذ كمقياس لسير التفاعل.
– إذا سمح للتفاعل أن يستمر حتى يتوقف تصاعد الأكسجين أي حتى يتم التفاعل فإن الحجم الكلي Voo لغاز الأكسجين عند نهاية التفاعل يتناسب مع عدد جزئيجرامات خامس أكسيد النيتروجين الموجود.
– أى أن Voo تكافئ a في المعادلة (10 – a) وبالمثل فإن حجم الأكسجين Vt والمقاس عند أى زمن t يتناسب مع عدد حزئيجرامات الأكسجين المتكون أي يكافئ x
– وتبعاً لهذا فإن تركيز خامس أكسيد النيتروجين المتبقي بعد زمن t أى (a – x) يكافئ (Voo – Vt) وبالتعويض عن هذة القيم يمكن حساب ثابت السرعة:
– إقرأ هذة الموضوعات المهمة كما يلي: (أضغط على الموضوع الذي تريده)
(1) رتبة التفاعل Order of reaction
(2) تفاعلات الرتبة الصفرية Zero order reaction
(3) تفاعلات الرتبة الأولي First order reaction
(4) تفاعلات الرتبة الثانية Second order reaction
(5) تفاعلات الرتبة االثالثة Third order reaction
(6) طرق تعيين رتبة التفاعل Determining of Order reaction
(7) مسائل محلولة على رتبة التفاعل Solved Problems On Order reaction
المراجع : – الكيمياء الحركية والكهربية.محمد مجدي عبد الله واصل. ، الطبعة لأولى (1425هـ – 2004م) / دار النشر للجامعات – القاهرة – جمهورية مصر العربية