أسئلة وإجاباتالكيمياء العامة
مسائل محلولة على خواص الغازات Gas Properties – الجزء الثاني
يمكنك متابعة الجزء الأول من مسائل محلولة على خواص الغاز المثالي من خلال هذا الرابط : الجزء الأول
مثال (11):
(أ) احسب معدل الطاقة الحركية (1 mol) من غاز مثالي عند درجة حرارة (25 Co).
(ب) احسب معدل الطاقة الحركیة لجزيء واحد من ھذا الغاز المثالي.
الحل:
(أ) باستخدام العلاقة:

(ب) المعدل السابق للحركة (3716.360 J) لمول واحد من الغاز المثالي. والمول الواحد یحوي عدد أفوجادرو من جزیئات الغاز (N= 6.023 × 1023) وبالتالي فإن معدل الطاقة الحركية لجزيء واحد من الغاز المثالي:
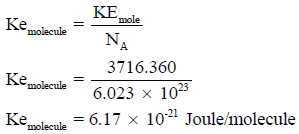
مثال (12):
احسب كثافة الغاز بوحدة (Kg/m3) عند ضغط (105 N/m2) عندما يكون الجذر التربيعي لسرعة جزيئاته هو ((3 × 102 m/s
الحل:
من النظریة الحركیة لجزیئات الغاز أمكن اشتقاق المعادلة التالیة:
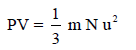
وتعرف ھذه المعادلة بالمعادلة الحركیة للغازات المثالیة.
ویمكن كتابة التعبیر الأخیر لضغط الغاز بصورة بدیلة، حیث (mN) هى الكتلة الكلية للغاز ،(V) هي الحجم الكلي ، وبذلك فإن الكثافة (d) تساوي (mN/V) وتصبح المعادلة كمايلي:
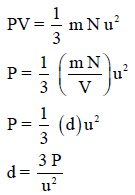
ووحدة الضغط ھنا ھي:
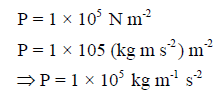
وبالتالي لحساب الكثافة نعوض في العلاقة السابقة باستخدام وحدات الضغط (Kg m-1 s-2)
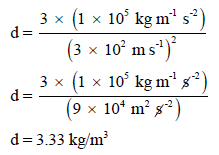
مثال (13):
(100 g) من خلیط من غازي النيتروجين والمیثان یحتوي على (31.014 %) وزناً من النیتروجین ویشغل حجماً مقداره (0.99456) لتر عند ضغط محدد وفي درجة (50 Co)احسب الضغط الجزئي لكل غاز والضغط الكلي للخلیط.
الحل:
– نحسب أولا وزن غاز النیتروجین والمیثان وفقاً لنسبتھما كما یلي:
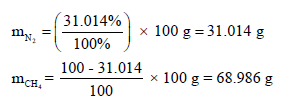
– نحسب عدد المولات:
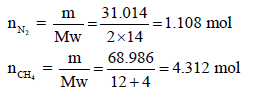
– بتطبیق القانون العام للغازات المثالیة یمكن حساب ضغط كل غاز على حدة كمایلي:

– یحسب ضغط غاز المیثان بنفس الطریقة:
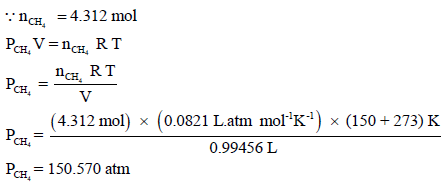
– لحساب الضغط الكلي للغاز في الوعاء فإنه یمكن إتباع إحدى طریقتین:
الطريقة الأولى:
بتطبیق قانون دالتون للضغوط الجزئیة والذي ینص على أن الضغط الكلي للغازات في وعاء یساوي مجموع الضغوط الجزئیة لتلك الغازات:
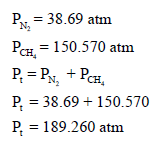
الطريقة الثانية:
بتطبیق القانون العام للغازات المثالیة باستخدام عدد المولات الكلي (nt):

بتطبیق القانون العام للغازات المثالیة:
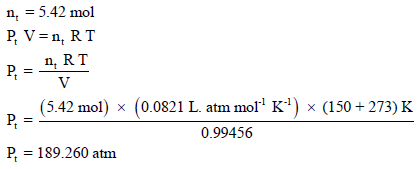
مثال (14):
تم جمع غاز مثالي فوق الماء عند درجة حرارة (25 Co) مما تسبب في تشبعه ببخار الماء فإذا كان حجم الغاز (190 cm3) والضغط الكلي (740 mmHg) وإن الضغط الجزئي لبخار الماء في الخلیط مساو للضغط البخاري للماء عند درجة حرارة (25 Co)ويساوي (24 mmHg) احسب حجم الغاز الجاف dry gasعند ضغط له یساوي (760 mmHg) فارضاً أن بخار الماء والغاز مثالیا السلوك.
الحل:
أولاً نحسب ضغط الغاز الجاف عندما كان الحجم (V= 190 cm3) من قانون دالتون للضغوط الجزئية:
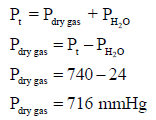
فإذا فرضنا أن ضغط هذا الغاز هو (P1= 716 mmHg) والحجم (V1= 190 cm3) وبالتالي فإن ضغط الغاز في الحالة الثانیة ھو (P2 = 760 mmHg) عند حجم (V2)
ولحساب الحجم (V2) نطبق قانون بويل:
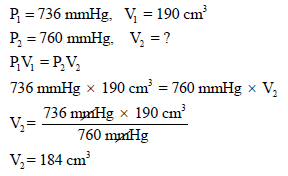
مثال (15):
خليط يتكون من (0.495 g) من الغاز (A) الذي وزنه الجزيئي (66 g/mol) و (0.182 g) من الغاز (B) والذى وزنه الجزيئي (45.5 g/mol) وأن الضغط الكلي لهما هو (76.2 cmHg) احسب الضغط الجزئي للغازين؟
الحل:
– نوجد أولاً عدد المولات ومنه ونوجد الكسر المولي لكل غاز:
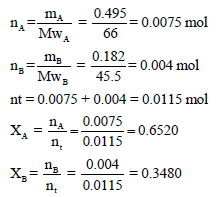
– لحساب الضغط الجزئي للغاز A نتبع العلاقة التالية:
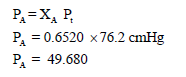
– بنفس القانون نحسب الضغط الجزئي للغاز B:

– للتأكد من أن الضغوط الجزئیة المحسوبة صحیحة فإننا نقوم بجمع ھذه الضغوط:
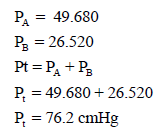
ونلاحظ أن المجموع الكلي المحسوب یساوي الضغط الكلي الوارد في المسألة.
مثال (16):
تم استخدام الطریقة المشبعة لحساب الضغط البخاري للكلوروبكرین (Chloropicrin (CCl3NO2 وكانت النتائج كما یلي:
احسب الضغط البخاري للمادة.
(علماً بأن الكتل الذرية:(C= 12 , Cl= 35.5, N= 14, O= 16)
R= 0.0821 L. atm mol-1 K-1
الحل:
– بتطبیق قانون دالتون للضغوط الجزئیة:
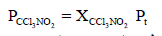
– وبالتالي نحسب أولاً الكسر المولي:
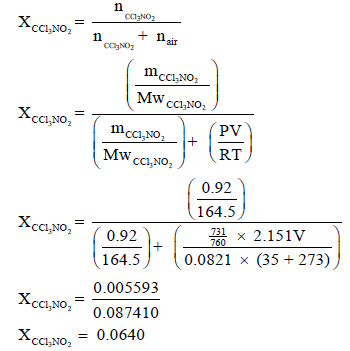
– وبالتالي یمكن حساب الضغط الجزئي للغاز كما یلي:
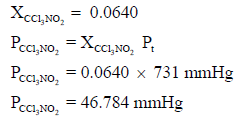
مثال (17):
مصباح وزنه (30.2341 g) عندما يكون فارغاً من الهواء ووزنه (30.6771 g) عندما يملأ بغاز (N2O) بينما يكون وزنه (270 g) عندما يملأ بالماء وعند درجة حرارة (15 Co) وضغط (740 mmHg) بافتراض أن سلوك الغازات مثالي.
احسب الوزن الجزيئي للغاز N2O عملياً وقارنه بالوزن الجزيئي نظرياً؟
علماً بأن كثافة الماء (1 g/cm3) و (R = 0.0821 L.atm mol-1 K-1) والكتل الذرية: (N= 14, O= 16)
الحل:
– نحسب أولاً وزن الغاز N2O وذلك بالفرق بین وزن المصباح الفارغ ووزن المصباح وھو مليء بغاز N2O:
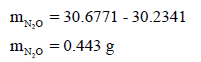
– ووزن الماء الذي ملء به المصباح یساوي:
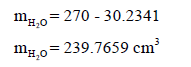
– نستفید من ملأ المصباح بالماء في معرفة حجمه من خلال العلاقة بین الوزن والحجم والكثافة:
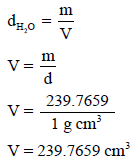
– بالتالي یمكن معرفة الوزن الجزیئي للغاز من خلال القانون العام للغازات المثالیة:
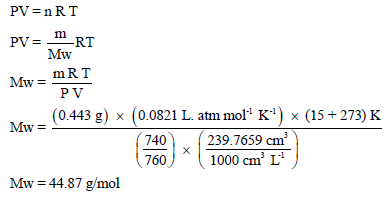
– للتأكد من ھذا الجواب نوجد الوزن الجزیئي نظریاً من خلال مجموع الكتل الذریة:
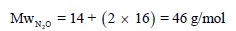
ونلاحظ أن القیمتین التجریبیة (العملیة) والنظریة متقاربة.
مثال (18):
في تجربة فیكتور مایر لحساب الوزن الجزیئي تم تبخیر (0.152 g) من مركب له الصيغة العامة (C4H5)n وقد أزاح حجماً مقداره (36.0 cm3) فوق الماء عند درجة حرارة (16 Co) وأن الضغط الجوي (764 mmHg) والضغط البخاري للماء في هذه الدرجة هو (13.6 mmHg).
احسب الوزن الجزیئي للمركب وما صیغته الجزیئیة؟
الحل:
– نحسب ضغط بخار الغاز باتباع قانون دالتون للضغوط الجزئیة:
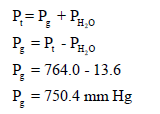
– بتطبیق معادلة الغاز المثالي یمكن حساب عدد مولات الغاز:
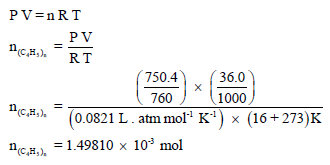
– من معرفة وزن الغاز المتبخر وعدد الم ولات یمكن حساب الوزن الجزیئي للغاز كما یلي:
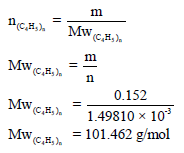
– لحساب قيمة (n) في الصيغة (C4H5)n من خلال الوزن الجزيئي المحسوب (101.462
g/mol):
g/mol):
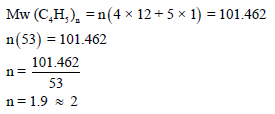
– بالتالي فإن المركب تكون صیغته الجزیئیة ھي:
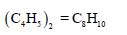
مثال (19):
إذا كانت كثافة الآرجون (Ar)السائل (1.40 g/cm3) عند درجة غليانه البالغة (-186 Co) احسب الزيادة في الحجم عندما يحول (1 mol) منه إلى بخار في درجة الغليان وضغط (1 atm) فارضاً السلوك المثالي.
الحل:
– أولاً نحسب حجم الآرجون السائل من البیانات المعطاة في المسألة عن وزن وكثافة الآرجون:
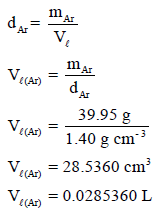
وھذا یمثل حجم الآرجون السائل.
– لحساب حجم مول واحد من غاز الآرجون فإننا نطبق القانون العام للغاز المثالي:
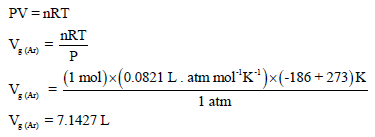
– وبالتالي فإنه لحساب الزیادة في الحجم عندما یحول سائل الآرجون (1 mol Ar) إلى بخار:
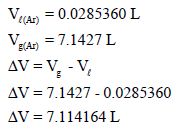
ویتضح أن حجم السائل قلیل جداً مقارنة مع حجم البخار.
مثال (20):
احسب الوزن الجزيئي لمادة عضوية مجهولة في حالة تبخر (0.1525 g) من السائل فإن البخار يشغل حجماً قدره (35.05 cm3) في درجة حرارة (20 Co) وضغط (730 mmHg) وأن التحليل الكيماوى للمادة كما يلى:
ثم احسب الصیغة الجزیئیة للمركب فارضاً أن الغاز مثالي السلوك.
علماً بأن (R = 0.0821 L.atm mol-1 K-1)والكتل الذرية: (C= 12, H= 1 , Br= 79.9)
الحل:
– نحسب أولاً عدد المولات من الغاز باستخدام قانون الغاز المثالي:
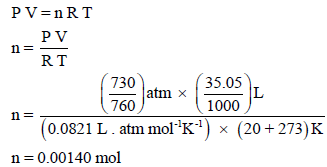
– من عدد المولات یمكن حساب الوزن الجزیئي كما یلي:
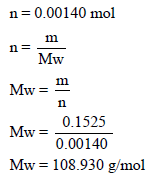
– لمعرفة الصیغة الجزیئیة فإننا نوجد وزن كل عنصر كما یلي:
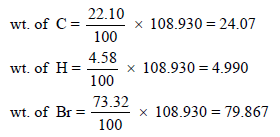
– بقسمة الوزن السابق على الوزن الذري لكل عنصر نحصل على:
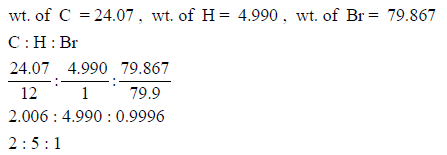
وبالتالي فإن الصیغة الجزیئیة تكون C2H5Br والتى لها الوزن الجزيئي (108.9 g/mol)
المراجع: أسس الكيمياء العامة والفيزيائية – الجزء الأول.عمر بن عبد الله الهزازي ، قسم الكيمياء- كلية العلوم – جامعة أم القرى – المملكة العربية السعودية.