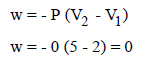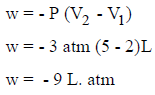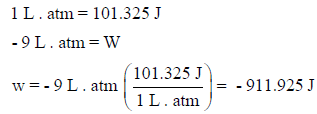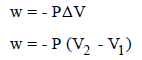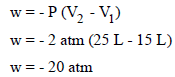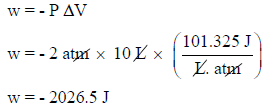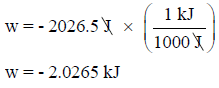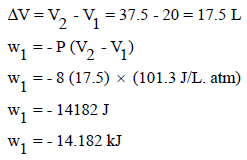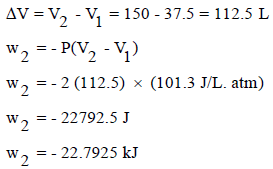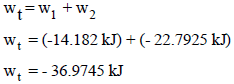الشغل – حساب الشغل (الديناميكا الحرارية) + مسائل محلولة

تعريف الشغل الميكانيكي Mechanical work

– الشغل الميكانيكى هو حاصل ضرب القوة في الإزاحة ويرمز له بالرمز (w) حيث:

w = FΔL 

– ولكن معناه في علم الثیرمودینامیك أوسع من ذلك حیث یشتمل على الشغل المیكانیكي المبذول ضد الجاذبیة الأرضیة والشغـل الكھربي (electrical work) الخ.

– سنركز في ھذا الشرح على الشغـل الناتج عن التغیر في حجم كمیة معینة من غاز تحت ظروف معینة.

اشتقاق قانون الشغل الميكانيكي الناتج من تغير الحجم عند ضغط ثابت

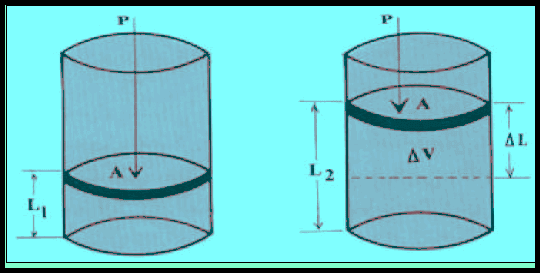
– إذا افترض وجود غاز في اسطوانة مزودة بمكبس متحرك عدیم الوزن والاحتكاك مساحة سطحه (A) عند ظروف معینة من الحجم والضغط ودرجة الحرارة.

– فعند تمدد الغاز فإنه یدفع المكبس الى أعلى ضد ضغط مضاد (P) معاكس لاتجاه التغير (الضغط الجوي مثلاً) منجزاً شغلاً ضد المحیط.

– وبما أن الضغط یعرف بأنه القوة المسلطة على وحدة المساحات كما يلي:

P = F/A 

F = PA

– وبما أن:

w = FΔL

 – وبالتعويض عن قيمة F من المعادلة: F = PA  في المعادلة: w = FΔL نحصل على الشغـل المنجز نتیجة للتمدد كما يلي:

F = PA

w = F ΔL

w = P A ΔL

– وحیث أن المكبس ینزاح باتجاه معاكس لاتجاه القوة فإن التغیر في الحجم Δv)) یساوي حاصل ضرب مساحة المقطع (A) في الإزاحة (ΔL) مسبوقة بإشارة سالب كما يلي:

ΔV = – A ΔL

 – ومن المعادلتين السابقتين نستنتج أن الشغل يمكن حسابة بواسطة العلاقة الآتية كما يلي:

w = – PΔV

 – ويمكن كتابة المعادلة إيضاً على الصورة الآتية كما يلي:

w = – P (V₂ – V₁)

V₁: الحجم الابتدائي للغاز

V₂: الحجم النهائي للغاز

– والإشارة السالبة تدل على أن طاقة النظام تنخفض عندما یزداد الحجم أي أن النظام یعمل شغـل على المحیط.

ملاحظات هامة على قانون الشغل: w = – P (V₂ – V₁)

(1) إذا كان قيمة الضغط المضاد أو الخارجي (P) أصغر من ضغط الغاز

– فإن الغاز يتمدد ضد المحيط

– وتكون (V₂ > V₁) وبالتالي فإن ΔV موجبة.

– وبذلك تكون قيمة الشغل (w) سالبة.

– أي أن النظام أنجز شغلاً على المحيط (النظام فقد طاقة كشغل)

(2) إذا كان ضغط المحیط أكبر من ضغط الغاز

– فإن الغاز ینكمش وفي ھذه الحالة یكون الضغط المضاد ھو ضغط الغاز نفسه لأنه یعاكس اتجاه التغیر

– وتكون (V₂ < V₁) وبالتالي فإن ΔV تصبح سالبة.

– وعلى ذلك تكون قيمة الشغل (w) موجبة.

– أي أن المحيط يعمل شغلاً على النظام (تزداد طاقة النظام بسبب الشغل الذي بذل علیه).

 – وبالتالي فإن الضغط ھو الذي یحدد مسار العملیة، مما یعني أن الشغل لیس تابعاً للحالة.( ليس دالة حالة)

(3) الشغل ليس دالة حالة

الشغل لیس تابع للحالة وذلك لأن الشغل یعتمد على الضغط. وذلك لأن الضغط ھو الذي یحدد مسار العملیة وهو ثابت.

مسائل محلولة على الشغل الميكانيكي

مثال (1)

إذا تمدد غاز مثالي عند درجة حرارة (25 C^o) من الحجم (2 L) إلى الحجم (5 L) عند ضغط ثابت فاحسب الشغل المنجز عندما یتمدد الغاز:

 (أ) ضد الفراغ

(ب) ضد ضغط ثابت مقداره (3 atm)

الحل:

(أ) التمدد ضد الفراغ:

یعني أن الضغط المضاد یساوي صفراً:

(ب) التمدد ضد ضغط ثابت مقداره (3 atm)

 ويفضل تحويل وحدات L.atm  إلى وحدات الجول حيث (1 L.atm = 101.3 J) 

مثال (2)

يتمدد غاز مثالي من حجم 15 L إلى 25 L ، وكان الضغط النهائي هو 2 atm ، احسب:

(أ) الشغل بوحدة (L.atm)

(ب) الشغـل بوحدة الجول (J)

(جـ) ما دلالة إشارة قيمة الشغل 

الحل: 

لحل ھذا المسألة نتبع العلاقة الآتية كما يلي:

(أ) حساب الشغـل بوحدة (L.atm)

(ب) حساب الشغل بوحدة الجول (J) : 1 L.atm = 101.3 J

 أما قیمة الشغـل السابقة بوحدة الكیلو جول kJ ھي كما يلي:

 أي لتحویل الجول الى وحدة الكیلو جول نقسم على (1000)

(جـ) إشارة قيمة الشغل ھنا بالسالب

مما یعني أن النظام فقد شغلاً (بذل شغلاً) على المحیط (ضد المحیط).

مثال (3)

أحسب الشغل بوحدة الجول عندما يتجمد ( (2 ml من الماء عند (0 C^o) وضغط جوي 1 atm) ) ليصبح حجمه (2.2 ml)

الحل:

نحسب أولاً التغیر في الحجم بالوحدة المعطاة في المسألة وھي المللتر (ml) ثم نحولھا الى وحدة اللتر (L)، حیث أن العلاقة بینھما كما يلي:

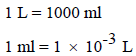
ویكون التغیر في الحجم كما يلي:

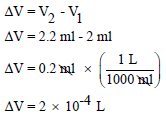
 وبالتالي یكون الشغل المبذول كما يلي:

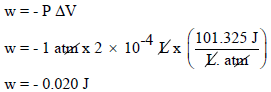
 وإشارة الشغـل بالسالب تعني أن النظام بذل شغلاً على المحیط.

مثال (4)

انتقل غاز من إناء حجمه (8 L) إلى إناء حجمه (3 L) تحت تأثير ضغط خارجي مقداره (4 atm). احسب الشغل المبذول خلال ھذه العملیة.

الحل:

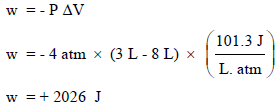
ونلاحظ أن الشغـل له قیمة موجبة، مما یعني أن المحیط بذل شغلاً على النظام.

مثال (5)

تكثف مول واحد من غاز CO₂ حسب المعادلة التالية:

CO_{2 (g)} → CO_{2 (L)}

في إناء حجمه (4 L) إلى سائل حجمه (350 cm³) عند ضغط مقداره (5 atm). وانطقلت حرارة مقدارها 392 kJ ، احسب الشغل المبذول؟

الحل:

نحسب التغیر في الحجم بعد تحویل وحدة السم^٣ الى وحدة اللتر كما يلي:

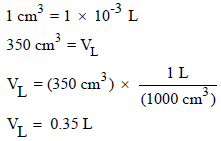
 وبالتالي فإن التغیر في الحجم كما يلي:

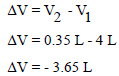
 وبالتالي فإن الشغل المبذول كما يلي:

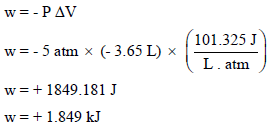
 وبما أن إشارة الشغـل بالموجب فإن المحیط بذل شغلاً على النظام.

مثال (6)

تكثف مول واحد من غاز SO₂ في إناء حجمه (3 L) إلى سائل حجمه (300 cm³) عند ضغط مقداره (10 atm). وانطلقت حرارة مقدارها 393 kJ

(أ) أكتب المعادلة الكیمیائیة الحراریة

(ب) احسب الشغل المبذول.

الحل:

(أ) المعادلة الكیمیائیة الحراریة

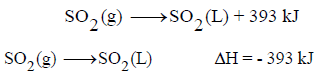
 (ب) الشغل المبذول

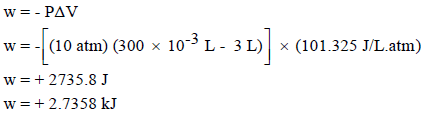
مثال (7)

حدد من خلال التفاعلات التالیة أي من المعادلات بذل فیه النظام شغلاً على المحیط مع التعلیل:

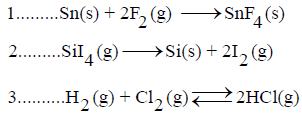
الحل :

القاعدة:

(1) عندما یكون عدد المولات الغازیة الناتجة (n_p) أكبر من عدد المولات الغازیة المتفاعلة (n_R) فإن ھذا یعني أن النظام قد زاد حجمه (تمدد) وبالتالي فإن النظام عمل شغلاً على المحیط.

(2) عندما یكون عدد المولات الغازیة الناتجة (n_p) أصغر من عدد المولات الغازیة المتفاعلة (n_R) فإن ھذا یعني أن النظام قد قل حجمه (انكمش) وبالتالي فإن المحيط عمل شغلاً على النظام.

(3) بالإضافة إلى ذلك عند تساوي عدد المولات الغازیة الناتجة والمتفاعلة فإن التغیر في الحجم یساوي صفراً وبالتالي لا یحدث شغل.

– وبتطبیق ھذا القواعد على التفاعلات كما يلي:

التفاعل الأول:

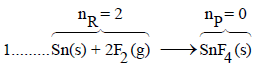
 بما أن (n_p < n_R) فإن الحجم قل وبالتالي فإن المحیط عمل شغلاً على النظام

التفاعل الثاني:

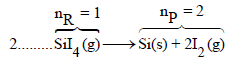
 بما أن (n_p > n_R) فإن الحجم قد زاد، وبالتالي فإن النظام یعمل شغلاً على المحیط.

التفاعل الثالث:

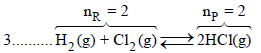
 بما أن (n_p = n_R) فإن الحجم لم یتغیر وبالتالي لا یحدث شغـل

مثال (8)

سمح لغاز مثالي حجمه (20 L) وضغطه (15 atm) بأن يتمدد على مرحلتين: الأولى كان الضغط الخارجي قدره (8 atm) الثانية كان الضغط الخارجي (2 atm) احسب الشغل الذي یبذله الغاز.

– يكون الحل على خطوتين كما يلي:

الحالة الأولى: حساب الشغل عندما یكون الضغط الخارجي (8 atm)

– المشكلة ھنا أنه لم یحدد الحجم النھائي الذي سیؤول إلیه الغاز بعد تمدده في المرحلة الأولى، لذلك فحساب الشغل غیر ممكن لأن الشغـل یعتمد على القانون كما يلي:

w = – P (V₂ – V₁)

– ولا سبیل الى ایجاد حجمه النھائي إلا بقانون بویل كما یلي:

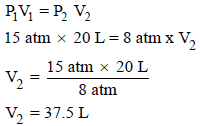
– وبالتالي فإنه یمكن حساب الشغل كما یلي:

الحالة الثانية: حساب الشغل عندما یكون الضغط الخارجي (2 atm)

– وفي ھذه الحالة نجد أن الحجم الإبتدائي (V₁ = 37.5 L) بینما الحجم النھائي غیر معلوم، وبالتالي یصعب حساب الشغل.

– وبنفس الطریقة فإننا نوجد الحجم النھائي (V₂) من قانون بویل كما يلي:

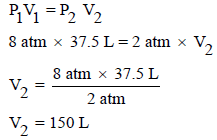
 وبالتالي فإنه یمكن حساب الشغـل كما یلي:

 – وبالتالي فإن الشغـل الكلي الذي یبذله الغاز في كلا المرحلتین كما يلي:

المراجع: أسس الكيمياء العامة والفيزيائية – الجزء الأول.عمر بن عبد الله الهزازي ، قسم الكيمياء- كلية العلوم – جامعة أم القرى – المملكة العربية السعودية