أسئلة وإجاباتالكيمياء الفيزيائية
الطاقة الداخلية ΔE والإنثالبي Enthalpy ΔH + مسائل محلولة
في هذا الموضوع سوف ندرس العلاقة بين الطاقة الداخلية والإنثالبي Internal Energy and Enthalpy ، وجدير بالذكر أننا قد تكلمنا في الموضوعات السابقة عن القانون الأول للديناميكا الحرارية وكيفية اشتقاق المعادلة الآتية:
ΔE = q – PΔV
العلاقة بين الطاقة الداخلية والإنثالبي Internal Energy and Enthalpy
(1) عند إجراء تفاعل عند حجم ثابت (ΔV = 0)
أي أن (ΔV = 0) فإنه لن ینجز شغلاً نتیجة للتغیر الكیمیائي، وبالتالي فالمعادلة:
ΔE = q – PΔV
وتصبح :
ΔE = qv
– المعادلة الأخيرة تبين أن حرارة التفاعل تساوي الفرق بین طاقة المواد الناتجة والمتفاعلة (أي تساوي التغیر في الطاقة الداخلیة للنظام)، وھذا ما یحدث عند قیاس حرارة التفاعل عند حجم ثابت باستخدام المسعر.
(2) عند إجراء تفاعل عند ضغط ثابت
– عند إجراء تفاعل عند ضغط ثابت حدوث تغیر ملحوظ في الحجم نتیجة اشتراك بعض المواد الغازیة سواء كانت متفاعلة أو ناتجة أو كلاهما، بالتالي لا يمكن إهمال الحد (PΔV) في المعادلة:
ΔE = q – PΔV
حيث أن حرارة التفاعل (q) لا تساوي فقط (ΔE)
– فإذا افترضنا أن:
ER: طاقة المواد المتفاعلة ، Ep: طاقة المواد الناتجة.
VR: حجم المواد المتفاعلة الغازیة ، Vp: حجم المواد الناتجة الغازیة.
وبالتالي فإن:
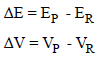
وبإعادة تنظیم المعادلة:
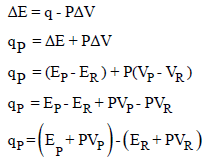
أي أن (qp) تساوي التغير في الخاصية (E + PV) عندما يحدث التفاعل ، و سميت هذه الخاصية بالإنثالبي Enthalpy ورمزها (H) حيث:
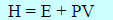
ووحدة الإنثالبي ھي وحدة الطاقة لأن E و PV لهما وحدات الطاقة وبما أن E ، P ، V توابع للحالة فإن H تابع للحالة
– المعادلة:
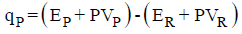
یمكن كتابتھا على النحو التالي:
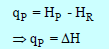
Hp: انثالبي المواد الناتجة ، HR: انثالبي المواد المتفاعلة
ΔH: تمثل التغیر في الإنثالبي Enthalpy وھو یساوي الفرق بین انثالبي المواد الناتجة وإنثالبي المواد المتفاعلة.
– والمعادلة: qp = ΔH تبین أن حرارة التفاعل عند ضغط ثابت تساوي التغیر في الإنثالبي.
وبدمج المعادلتین:
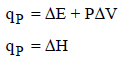
وهذا يعنى أن:
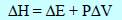
وھذا القانون یستخدم فقط عندما یكون الضغط ثابتاً.
الحالات الخاصة للمعادلة ΔH = ΔE + PΔV
(1) تفاعلات تشترك فيها مواد غازية حيث :(nR ≠ nP)
– فیھا تكون تغیرات الحجم كبیرة ولا یمكن إھمالھا، وبفرض سلوك الغازات سلوكاً مثالیاً فإن:
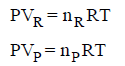
حیث أن:
np: عدد المولات الغازية الناتجة
nR: عدد مولات المواد الغازية المتفاعلة (عند ضغط ودرجة حرارة ثابتين)
R: ثابت الغازات العام (8.314 J/K.mol)
T: درجة الحرارة بالكلفن (K)
– من المعادلة:
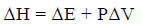
– فإننا سنجري تحویراً على القیمة PΔV كما يلي:
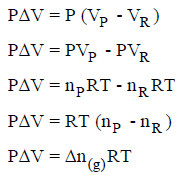
وبالتعويض بـــ PΔV = Δn(g) RT في المعادلة ΔH = ΔE + PΔV نحصل على:
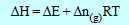
حيث أن Δn(g): التغیر في عدد المولات الغازية ، كما يمثل الفرق بين عدد المولات الغازية الناتجة والمتفاعلة.
(2) تفاعلات تشترك فيها غازات متفاعلة وناتجة حيث :(nR = nP)
وبالتالي فقيمة (Δn = 0) وحينئذ تؤول المعادلة:
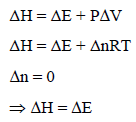
(3) تفاعلات تشترك فيها مواد صلبة أو سائلة فقط ( لا تشترك فيها مواد غازية):
تكون فیھا تغیرات الحجم صغیرة (ΔV ~ 0) وبالتالي یمكن إھمالھا، حینئذ تؤول المعادلة، وبالتالي يمكن إهمالها ، حيئنذ تؤول المعادلة ΔH = ΔE + PΔV إلي:
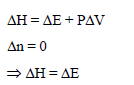
ملخص للعلاقة الریاضیة بین التغیر في الإنثالبي والتغیر في الطاقة الداخلیة لتفاعلات تشترك فیھا غازات وأخرى لا تشارك بھا غازات

مسائل محلولة على الطاقة الداخلية ΔE والإنثالبي Enthalpy ΔH
مثال (1): إذا علمت أن التغیرات الكیمیائیة والفیزیائیة التالیة تحدث عند ضغط ثابت، فحدد في كل مرة ھل الشغل یعمل من قبل النظام على المحیط أو یعمل من قبل المحیط على النظام، أو أن كمیة الشغل مھملة:
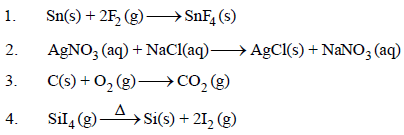
الحل:
(1)
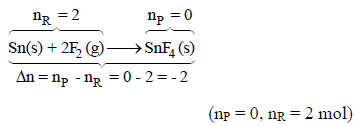
فالنظام حجمه سیقل لذلك فإن المحیط یعمل شغلاً على النظام.
(2)
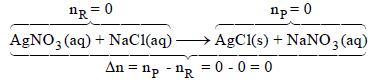
حیث أنه لا یوجد مواد غازیة متفاعلة أو ناتجة مشتركة فإنه یمكن إھمال الشغل.
(3)
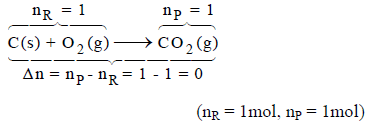
حیث یوجد مول واحد من المواد المتفاعلة الغازیة ومول واحد من المواد الغازیة الناتجة فإن (ΔV = 0) وبالتالي كمیة الشغل تساوي صفراً.
(4)
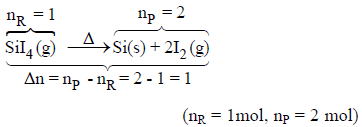
حیث أن مول واحد من المواد المتفاعلة ینتج مولین من المواد الناتجة الغازیة فإن حجم النظام یزداد ولذلك فإن النظام یعمل شغلاً على المحیط.
مثال (2): إذا كان التغیر في الطاقة الداخلیة یساوي (-333 kJ) للتفاعل التالي:
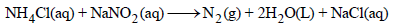
عندما ینتج مول واحد من N2 فإذا كان إنتاج مول واحد من النیتروجین یجعل النظام یزداد بمقدار (22.4 L) عند ضغط جوي واحد. فاحسب التغیر في إنثالبي ھذا التفاعل؟
الحل:
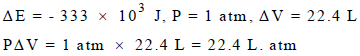
لتحويل القيمة 22.4 L.atm إلى وحدة الجول نضرب هذه القيمة بـــ 101.3
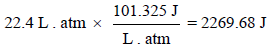
وبتطبيق العلاقة:
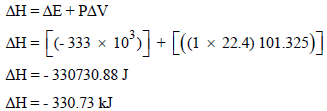
وفي الخطوة الأخيرة قمنا بتحويل وحدة (J) إلى (KJ) وذلك بقسمة الجول على (1000) حيث (1 kJ = 1000 J)
مثال (3): إذا كانت الحرارة المصاحبة لاحتراق مول واحد من البنزين تساوي (-3264.3 kJ) عند حجم ثابت ودرجة حرارة (298 K) فاحسب التغير في الإنثالبي (ΔH) للتفاعل، إذا علمت أن البنزين يحترق بوجود الأكسجين حسب المعادلة:
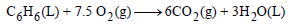
علماً بأن قیمة: .(R = 8.314 J/mol K)
الحل:
كمیة الحرارة عند حجم ثابت تعبر عن الطاقة الداخلیة :
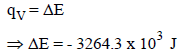
ولحساب التغیر في عدد المولات :
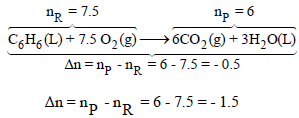
ولحساب التغیر في الانثالبي نتبع العلاقة:
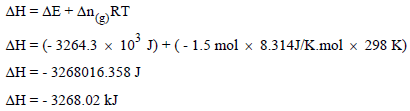
ملحوظة:
:ΔE یقاس عند حجم ثابت ودرجة حرارة ثابتة.
ΔH: یقاس عند ضغط ثابت ودرجة حرارة ثابتة.
مثال (4): أحسب التغیر في الطاقة الداخلیة للتفاعل:
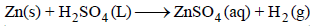
إذا كانت الحرارة المنطلقة هي 34200 Cal من الخارصين عند درجة حرارة 17 Co (علماً بأن R= 2 Cal /mol.K)
الحل:
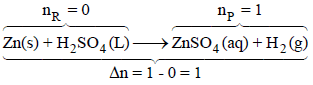
بتطبیق العلاقة:
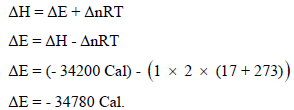
ويمكن حل المسألة بالجول بدلاً من الكالوري حيث (1 Cal = 4.184 J) وبالتالي فإن الحرارة المنطلقة هي:
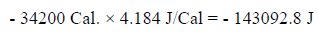
وقيمة R= 8.314 J/mol.K وبالتالي فإن:

مثال (5): احسب qp للتفاعل التالي:
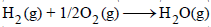
إذا كانت الحرارة المتصاعدة لهذا التفاعل تحت حجم ثابت هي 57507 Cal عند حرارة (0 Co) علماً بأن (R= 2 Cal/mol.k)
الحل:
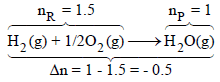
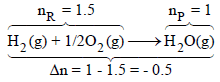
مثال (6): ما العلاقة بين (ΔE , ΔH) للتفاعل التالي:
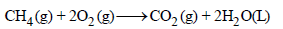
الحل:
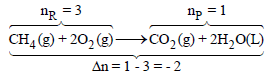
بتطبیق العلاقة:
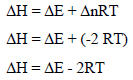
المراجع: أسس الكيمياء العامة والفيزيائية – الجزء الأول.عمر بن عبد الله الهزازي ، قسم الكيمياء- كلية العلوم – جامعة أم القرى – المملكة العربية السعودية