الكيمياء العامة
مناقشة فروض النظرية الحركية الجزيئية للغازات

تكلمنا في الموضوع السابق عن فروض النظرية الحركية الجزيئية للغازات Assumptions of Molecular Kinetic Theory of Gases . وفى هذا الدرس سوف نناقش تلك الفروض بالتفصيل:
مناقشة فروض النظرية الحركية الجزيئية للغازات
Discussion of Assumptions of Molecular Kinetic Theory of Gases
الافتراض الأول (تعريف الغاز)
(1) یتألف الغاز من جسیمات (دقائق) تسمى جزیئات، بعیدة عن بعضھا، وذات حجم صغیر جداً لدرجة أن الحجم الفعلي للجزیئات یكون مھملاً مقارنة بالحیز الموجود بین جزیئاتھا أو مقارنة بحجم الإناء الذي توجد فیه.
– هذا الإقتراح يكون معقولاً، من حقيقة أن انضغاطية الغازات تكون كبيرة جداً.
– توضح الحسابات أنه في غاز الأكسجين مثلاً عند (STP) يكون (99.96%) من الحجم الكلي عبارة عن حيز خال في أى لحظة. حيث أنه يوجد (2.7 x 1019 molecules/ml) من غاز الأكسجين عند (STP) فإن المسافة بين الجزئيات تكون حوالي (3.7 x 10-7 cm) والتي هي عبارة عن (12) مرة مثل القطر الجزيئي. وعندما یضغط الأكسجین أو أي غاز آخر فإن متوسط المسافة بین الجزیئات سوف یختزل، أي ینقص الكسر من الحیز الحر.
الافتراض الثاني (عدم وجود قوى تجاذب أو تنافر)
(2) لا یوجد قوى تجاذب (أو تنافر) بین جسيمات الغاز أو مع جدران الإناء الذي توجد به وتكون الجزيئات مستقلة تماماً عن الأخرى.
– من ملاحظة أن الغازات تتمدد تلقائیاً لتشغل كل الحجم المتاح لھا. ویحدث ھذا السلوك حتى بالنسبة للغاز المضغوط لدرجة كبیرة، حیث تكون الجزیئات ملاصقة لبعضھا البعض الى حد ما، ویجب أن تكون أي قوى بین الجزیئات ھي الأعظم.
– من الجدیر بالذكر أنه یجب أن لا یوجد ترابط یمكن تقدیره بین جزيء غاز وجیرانه.
الافتراض الثالث (التصادمات المرنة)
(3) تتحرك جسيمات الغاز بحركة سريعة مستمرة وعشوائية في خطوط مستقيمة لا يتغير اتجاهها إلا عن اصطدامها ببعضها أو مع جدران الإناء الحاوي. اصطدامات الجزیئات ببعضها اصطدامات مرنة، أي لا تفقد طاقة عند تصادمھا.
– إن الملاحظة الخاصة بالحركة البراونية، تدل ضمناً على أن جزئيات الغاز تتحرك متفقة مع الافتراض الثالث.
– مثل أى جسيم متحرك، فأن الجزئيات لها كمية من طاقة الحركة تساوي (1/2mu2) حيث (m) كتلة الجزيء، (u)سرعة الجزيء.
– تلك الجزئيات تتحرك في خطوط مستقيمة، إنما ينبع من افتراض عدم وجود قوى تجاذب. ولو أنه كان هناك قوي تجاذب بينها لأمكن للجزئيات أن تنحنى عن مسارات الخط المستقيم.
– نظراً لأنه يوجد جزئيات كثيرة إلى حد بعيد في عينة غاز، وبسبب أنها تتحرك سريعاً جداً (عند 0 Co تكون السرعة المتوسطة لجزئيات الأكسجين حوالي 1000 mph) فإنه یوجد تصادمات متكررة الحدوث.
– ومن الضروري اعتبار أن التصادمات تكون تامة المرونة، وذلك حیث أنھا لا تفقد طاقة حركة عن طريق التحول إلى طاقة وضع (مثلاً عند تشوية الجزئيات) وإذا لم يكن ذلك حقيقاً فإن حركة الجزئيات سوف تقف في آخر الأمر، كما أن الجزيئات سوف ترسب الى قاع الإناء الحاوي.
الافتراض الرابع (طاقة الحركة)
(4) عند لحظة معينة، فأنه في أي تجمع لجزئيات غاز، يوجد جزيئات مختلفة لها سرعات مختلفة، وطاقات حركة مختلفة وتتناسب متوسط الطاقة الحركية لكل جزیئات الغاز تناسباً طردیاً مع درجة الحرارة المطلقة.
– ھذا الإفتراض له شقان:
(أ) أنه یوجد توزیع لطاقة الحركة.
(ب) طاقة الحركة المتوسطة تتناسب مع درجة الحرارة المطلقة.
– يحدث التوزيع أو المدى للطاقات نتيجة للتصادمات الجزيئية التي تغير باستمرار من سرعة جزئ مفرد. إذ أن جزيئاً معيناً يمكنه أن يتحرك إلى الأمام بسرعة محددة إلى أن يرتطم بآخر الذي يفقد إلية بعضاً من طاقة حركته، وربما فيما بعد يلقى ارتطاماً من ثالث، ويكتسب طاقة حركة.
– هذا التبادل لطاقة الحركة بين الجيران يحدث باستمرار بحيث أن طاقة الحركة الكلية لعينة غاز هي التي تبقى كما هي بشرط أنه طبعاً لا تضاف طاقة لعينة الغاز من الخارج مثلاً بالتسخين أو تسحب منه طاقة مثلاً بالتبريد.
– وتتركب طاقة الحركة الكلیة لغاز من طاقات الحركة لجمیع الجزیئات التى يمكن أن يكون كل منهما متحركاً بسرعة مختلفة. وعند لحظة معينة يمكن لقليل من الجزئيات أن تقف ساكنة بدون طاقة حركة. وقد يكون لقليل طاقة حركة عالية، ويكون لمعظمها طاقة حركة قريبة من المتوسط ویتلخص الوضع في الشكل التالي:
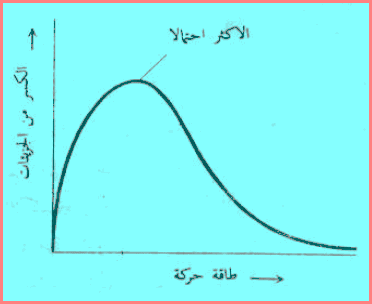 |
| توزيع الطاقة في غاز |
الشكل يوضح التوزيع العادي لطاقات الحركة في عينة غاز وتعبر كل نقطة على المنحنى عن أى كسر من الجزئيات تكون له قيمة معينة من طاقة الحركة.
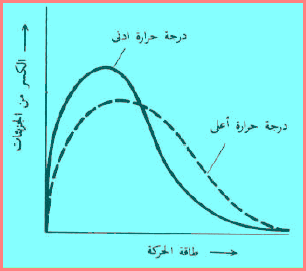
– يمكن أن ترتفع درجة حرارة غاز بإضافة حرارة. وماذا يحدث للجزيئات عندما ترفع درجة الحرارة؟ فالحرارة التي تضاف عبارة عن صورة للطاقة وبذلك فأنها یمكن أن تستخدم في زیادة سرعة الجزیئات، وبالتالي متوسط طاقة الحركة. ویوضح ذلك في الشكل التالي:
 |
| توزيع الطاقة فى غاز عند درجة حرارة |
الشكل يوضح عدد حيث يصف الخط المتقطع الوضع عند درجة حرارة أعلى. فعند درجة الحرارة الأعلى يكون للجزئيات متوسط طاقة حركة أعلى منها عند درجة حرارة أدني. وبذلك فإن درجة الحرارة تصلح كمقیاس لمتوسط طاقة الحركة.
المعادلة الأساسية للنظرية الحركية للغازات
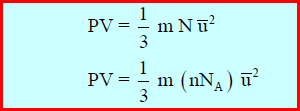
P: الضغط بوحدة Pa
V: الحجم بوحدة m3
N: عدد الجزئيات
m: كتلة الجزئ الواحد بوحدة Kg
u᷆2: متوسط مربع سرعة الجزئ بوحدة m2/s2
مثال محلول على فروض النظرية الحركية للغازات
احسب الضغط بوحدة kPa المبذول بواسطة (2 x 1021 molecules) من غاز النيتروجين في وعاء حجمه (1 L) علماً بأن متوسط مربع السرعة لهذة الجزيئات هو (244036m2/s2) (الكتلة الذرية لعنصر النيتروجين = (14
الحل:
نحسب أولاً كتلة ا لجزيء الواحد من غاز النیتروجین بوحدة Kg:
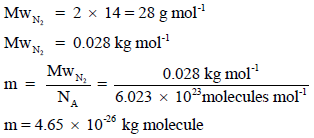
وبتطبیق المعادلة الأساسیة للنظریة الحركیة للغازات:
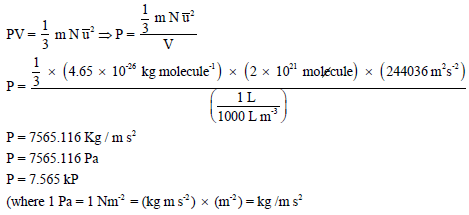
المراجع:
فروض النظرية الحركية للغازات – أسس الكيمياء العامة والفيزيائية – الجزء الأول. عمر بن عبد الله الهزازي ، قسم الكيمياء- كلية العلوم – جامعة أم القرى – المملكة العربية السعودية