حساب العدد الذري والعدد الكتلي ومتوسط الوزن الذري Calculation of Atomic Number, Mass Number and atomic weight

الكيمياء, الكيمياء العامة

 العدد الذري Atomic number

** هو عبارة عن عدد البروتونات الموجودة في نوية ذرة العنصر.ولما كانت ذرات العناصر المختلفة متعادلة كهربياً فهذا يعني أن عدد البروتونات = عدد الإلكترونات. لذلك يمكن القول أن:

العدد الذري (Z) = عدد البروتونات (P⁺) = عدد الإلكترونات (e^–)

** يعتبر العدد الذري من مميزات ذرات العنصر الواحد حيث لجميع ذرات العنصر الواحد نفس العدد الذري وهو يختلف عن العدد الذر لذرات العناصر الأخرى.

** العالم الانجليزي هنري موزلى هو أول من عين الأعداد الذرية لعدد من العناصر باستخدام أشعة اكس (X-rays)

العدد الكتلي Mass number

** هو مجموع أعداد البروتونات وأعداد النيترونات في نوية ذرة عنصر ما

العدد الكتلي (A)  = عدد البروتونات (P⁺)  + عدد النيترونات (n^o)

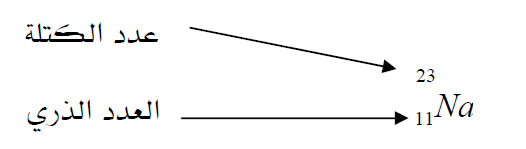
** لقد اتفق أن يكتب العدد الكتلي إلى يسار الرمز الكيميائي للعنصر وفي الزاوية العليا العدد الذري فيكتب إلى يسار الرمز الكيميائي وفى الزاوية السفلى للرمز: 

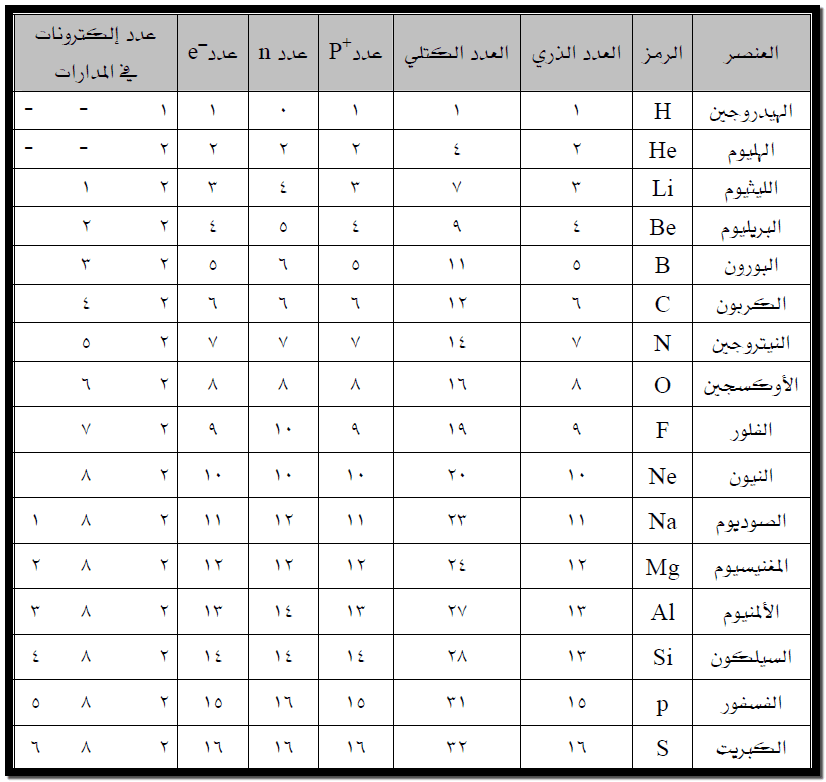
الجدول التالي يحتوي على القيم العددية لبعض المفاهيم ذات العلاقة بالتركيب الذري :

النظائر Isotopes

  حصل العالمان (Thomson
& Aston) عام (1912 -1913) عند دراسة تحديد نسبة (e/m) للأيونات الموجبة لغاز النيون Ne على نتائج غير متوقعة ولم يمكن تفسيرها
إلا إذا اعتبرنا أن 91% من الذرات لها وزن طبيعي و
9% من الذرات أثقل من الوزن الطبيعي، وقد أدى هذا الاكتشاف إلى
الحقيقة التالية:

إن ذرات العنصر الواحد يمكن أن تختلف كتلتها قليلاً عن بعضها
البعض وقد سميت هذه الذرات المختلفة في الوزن “النظائرIsotopes ” علماً أن لهذه الذرات
الصفات الكيميائية نفسها، إلا أن لها صفات إشعاعية مختلفة وأوزاناً ذرية مختلفة. وهذه
الحقيقة أدت إلى تعديلين في نظرية دالتون Dalton atomic Theory

  أدى اكتشاف النشاط الإشعاعي Radio activity إلى تعديل الافتراض الأول لدالتون وهو
أن ذرات العناصر لا تتغير ، كما أدى إلى تعديل الافتراض الثاني وهو أن ذرات العنصر
متساوية في الكتلة، واتضح من ذلك أن ذرات بعض العناصر يكون لها نفس العدد الذري
ولكن تختلف في أوزانها الذرية نظراً لوجود نظائر لهذه العناصر، هذه النظائر تكون
موجودة في كل عنصر بنسبة معينة تسمى الوفرة المئوية.

الخلاصة:

** النظائر هي مجموعة من ذرات نفس العنصر متطابقة فى الخواص
الكيميائية ومتساوية في العدد الذري ومختلفة فى العدد الكتلي، وهذا الاختلاف ناتج
من وجود أعداد مختلفة من النيترونات (n) في نويات هذه الذرات.

**معظم العناصر الكيميائية تتكون من نظيرين أو أكثر إلا أن هناك
عدداً قليلاً نسبياً (مثل: الفلور، الصوديوم، الألومنيوم) تتكون من نوع واحد من
الذرات، أي ليس لها نظير.

** مثال: تشكل عينة من غاز النيون من
ثلاث نظائر وحسب النسبية المئوية المبينة إلى جوار كل من هذه النظائر :

النظائر هي :

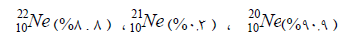
يلاحظ من هذه النسب أن نظير ²⁰Ne هو أكثر هذه العناصر وفرة فى الطبيعة، هذه
النسب ثابتة لا تتغير بتغير العينة أو بمعنى آخر من المستحيل أن تجد نسبة النظير ²²Ne –على سبيل المثال-
تساوي 10% فى عينة طبيعية.

وحدة الكتل الذرية Atomic
Mass Unit

** نظراً لصغر كتلة الذرة وبالتالي صغر القيمة العددية لهذه
الكتلة في حالة استخدام وحدة الكتلة المتعارف عليها (الجرام ومشتقاته) حيث اتفق
المكتب الدولي للقياسات عام 1961 على اعتبار ذرة الكربون ¹²C هي العيار Standard لقياس الأوزان الذرية
للعناصر واختيرت ذرة الكربون ووزنها (12 amu) وحدة وزنيه ذرية atomic mass unit وتوزن ذرات العناصر بالنسبة
لها استخدام وحدة نسبية تدعى وحدة كتلة الذرة والتي يرمز لها (amu)
كبديل عن وحدة الجرام ومشتقاته.

** يمكن تعريف وحدة كتلة الذرة على أنها
جزء من 12 من كتلة نظير الكربون 12 ولتوضيح ذلك دعنا نأخذ المثال التالي:

يقال أن وزن ذرة الهليوم He  تساوي 4 amu
فما المقصود بذلك؟ المقصود وزن ذرة الهليوم تساوي 4
× 1/12 من وزن نظير الكربون 12 ويمكن
القول أن وزن ذرة الهليوم هو 1/3 وزن ذرة نظير الكربون 12.

** تسمى وحدة كتلة الذرة أحياناً بوحدة الكتلة الموحدة (Unified Mass unit)  ويمز لها بالرمز U أو تسمى أحياناً بدالتون (Dalton

حساب متوسط الوزن
الذري لعنصر

  يمكن تعريف متوسط الوزن الذري لعنصر
بأنه متوسط أوزان نظائره الطبيعية، ويعتبر مطياف الكتلة Mass spectrometer أدق وسيلة لتعيين الأوزان
الذرية للعناصر.

  نجد أن الوزن الذري للكربون في
الجداول الدولية للأوزان الذرية 12.011 بينما وزن ذرة الكربون القياسية ¹²C = 12 amu ، وهنا يجب أن نفرق بين الوزنين الأول 12 amu وهو
وزن ذرة الكربون ¹²C  بينما الثاني هو الكربون الطبيعي الذي يحتوي
على كمية قليلة من الكربون ¹³C وكمية
أقل من الكربون ¹⁴C
بالإضافة إلى ¹²C بنسبة
98.892% وعلية يكون متوسط الوزن الذري للكربون 12.011 amu وتسمى النسبة المئوية لتواجد النظير في العنصر بالوفرة الطبيعية NA Natural Abundance وبتقسيمها على 100 نحصل على الوفرة الجزئية X  Fractional Abundance أذا
يكون :

X = NA/ 100

ومن ثم فإن مجموع الوفرة الجزئية
لنظائر أي عنصر تساوي الواحد ويكون متوسط الوزن الذري لأى عنصر كالتالي :

  = m₁ × x₁
+ m₂ × x₂ + m₃ × x₃ +……..الوزن الذري 

أى :

الوزن الذري = الوفرة % × الوزن الذري للنظير الأول +
الوفرة % × الوزن الذري للنظير الثاني + الوفرة % × الوزن الذري للنظير الثالث
+………. وهكذا

مثال: يتكون عنصر المغنسيوم من ثلاث نظائر طبيعية، الأوزان
الذرية والنسبة المئوية لوفرة هذه النظائر موضحة بالجدول التالي. أحسب الوزن الذري
أو معدل الوزن الذري لعنصر المغنسيوم؟

الوزن الذري = الوفرة % × الوزن الذري للنظير الأول +
الوفرة % × الوزن الذري للنظير الثاني + الوفرة % × الوزن الذري للنظير الثالث

٢٥٫٩٨٢٥٩ × ٠٫١١١٧ + ٢٤٫٩٨٥٨٤× ٠٫١٠١٣ + ٢٣٫٩٨٥٠٤× ٠٫٧٨٧٠ =

٢٫٩٠٢ + ٢٫٥٣١ + ١٨٫٨٨ =

 amu
٢٤٫٣١٣ =

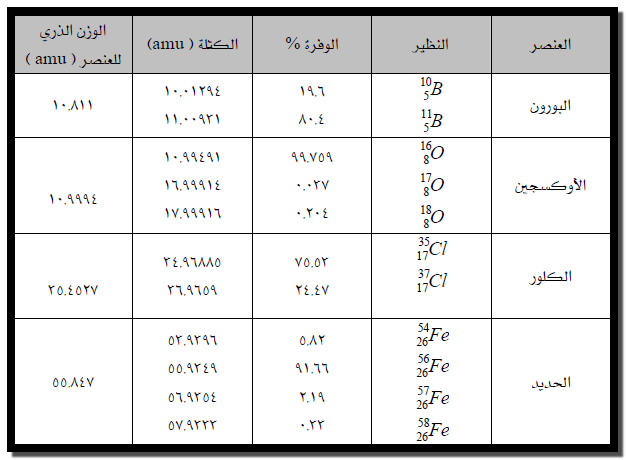
والجدول التالي يوضح نظائر بعض العناصر والوزن الذري لكل عنصر

 المراجع

 – إنتاج كيميائي – الكيمياء العامة – 180 كيم، الإدارة العامة لتصميم وتطوير المناهج- المملكة العربية السعودية.

 – مبادئ الكيمياء العامة (نظري – مسائل محلولة). محي الدين البكوش – نوري بسيبسو – ياسر حورية- نبيل شيخ قروش، الطبعة الثانية (2003م) / شركة الجا للنشر العلمي – طرابلس.