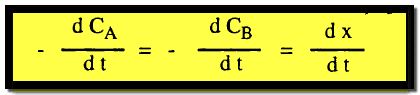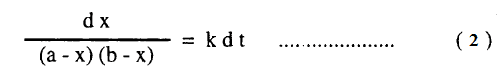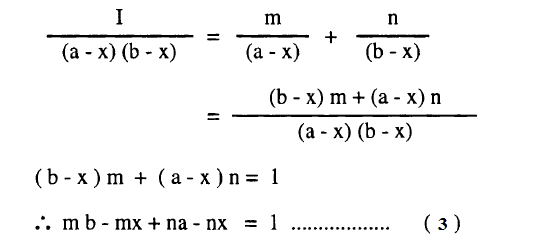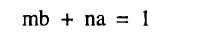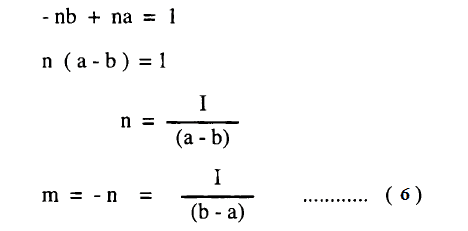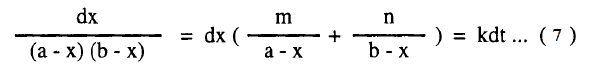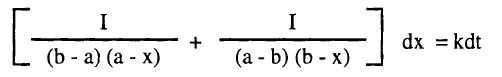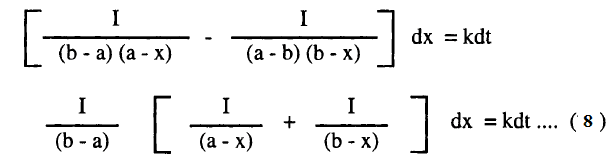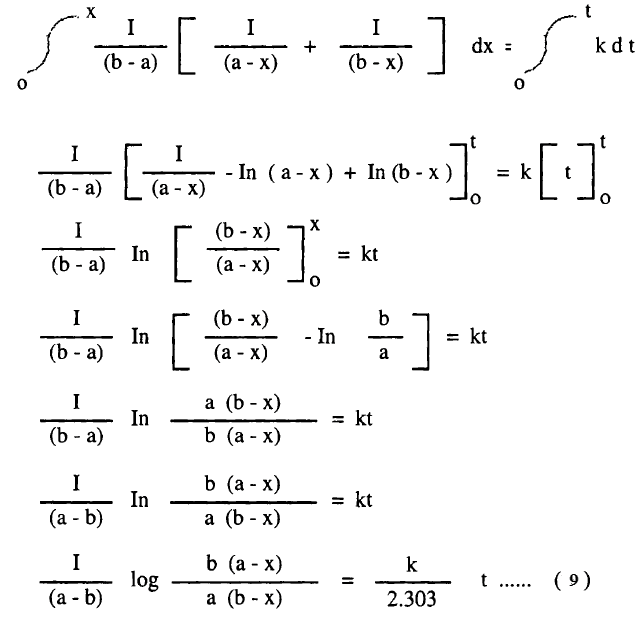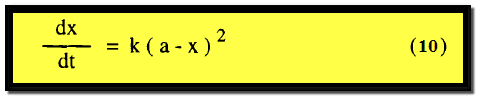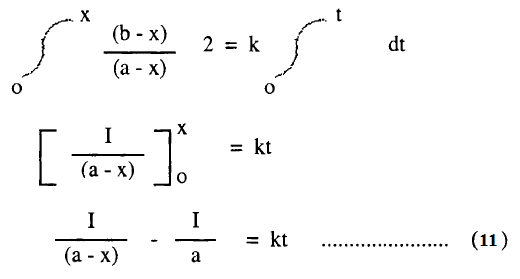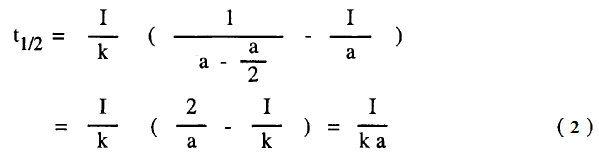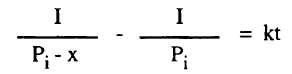تفاعلات الرتبة الثانية Second Order Reactions

تفاعلات الرتبة الثانية هي التفاعلات التي تعتمد فيها سرعة التفاعل على تركيزين ويوجد نوعان من هذه التفاعلات:

(1) النوع الأول:

ويمثل بالمعادلة العامة:

 A + B  → Products

حيث تتناسب سرعة التفاعل مع تركيز كل من المواد المتفاعلة مرفوعاً إلى أس واحد

Rate α C_AC_B

(2) النوع الثاني:

ويمثل بالمعادلة العامة:

   2A  → Products

حيث تتناسب سرعة التفاعل مع مربع تركيز المادة A أي أن:

Rate α C_A²

وفيما يلي سنعبر عن سرعة التفاعل في كل من الحالتين بمعلومية تركيز المواد المتفاعلة في زمن معين

استنتاج المعادلة الحركية لتفاعلات الرتبة الثانيـة

النوع الأول من تفاعلات الرتبة الثانيـة

A + B  → Products

وتمثل سرعة التفاعل كما يلي :

حيث dx/dt هي سرعة التفاعل بالنسبة لاختفاء أي من  A أو B وعلى هذا فأنه بالنسبة لتفاعل من الرتبة الثانية تكون السرعة :

حيث a ، b في التركيزات الأولية للمواد A ، B على التوالي، x هي تركيز المادة A أو B المتفاعلة في زمن t ، k هي ثابت السرعة للتفاعل ، ويمكن كتابة المعادلة (1) في الصورة الآتية:

ولتسهيل عملية التكامل لهذه المعادلة نعبر عن الحاصل 1/(a-x)(b-x) بمجموع الحدين الآتيين:

ويوضح معامل x = صفر

ويوضح معامل x = صفر في المعادلة (3)

ومن المعادلات (4) ، (5) ينتج أن:

وبالتعويض في المعادلة (2)

وبالتعويض من (6) في (7) كما يلي:

وبإجراء التكامل للمعادلة (8) بين الحدود x = 0 عند t = 0 ، x = x عند t = t

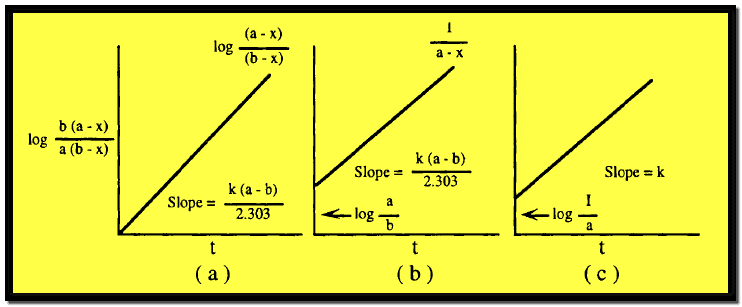
وهذه هي المعادلة الحركية لتفاعل من الرتبة الثانية يتضمن مادتين مختلفتين ويتضح منها أن رسم العلاقة بين  log b (a-x) / a (b-x) والزمن t يعطي خطاً مستقيماً ماراً بنقطة الأصل ، وله ميل يساوي k (a-b) / 2.303 كما هو مبين بالشكل التالي:

النوع الثاني من تفاعلات الرتبة الثانية

عندما تكون المادتان A ، B موجودتين بنفس التركيز الأول أي b = a أو عندما تكون A ، B هما نفس المادة كما في المعادلة العامة.

2A  → Products

ويكون التعبير عن السرعة كما يلي:

وبفصل المتغيرات وإجراء التكامل بين الحدود نحصل على :

برسم العلاقة بين 1/ (a-x)  مع الزمن له ميل يساويK  وتقاطع يساوي 1/a كما هو مبين في الشكل السابق رقم (C)

وحدات ثابت السرعة لتفاعلات الرتبة الثانيـة K 

يتضح من المعادلة رقم (11) أن وحدات K هي :

وبالتعبير عن التركيز بالجزئي جرام في اللتر والزمن بالثانية فإن :

K = 1 mole^-1 sec^-1

أي أن القيمة العددية لثابت السرعة في تفاعل الرتبة الثانية تختلف عن الرتبة الأولى في أنها تعتمد على التركيز.

فترة نصف العمر Half Life period

– تعرف فترة نصف العمر لأي تفاعل بأنها

(الزمن اللازم لكي ينخفض تركيز المادة المتفاعلة إلى نصف قيمته الأولية) أو (الزمن اللازم لإتمام نصف التفاعل)

حيث أنه في هذا التفاعل يزداد الضغط عند ثبوت الحجم يمكن دراسة سرعة التفاعل بقياس الزيادة في الضغط بمانومتر متصل بالوعاء الذي يحتوي التفاعل ويمكن حساب ثابت السرعة كالآتي:

نفرض أن: P_i هي الضغط الأولى للأسيتالدهيد ، x هي النقص في ضغطه بعد الزمن t أي أن ضغط الأسيتالدهيد عند زمن t يساوي (P_i – x) وعندما ينقص ضغط الأسيتالدهيد بالقيمة x فإن ضغط كل من الميثان وأول أكسيد الكربون يزداد بالقيمة x ويعبر عن الضغط الكلي للنظام كما يلي:

P = P_CH3CHO + P_CH4 + P_CO

= (P_i – x) + x + x

= P_i + x

⸫ x = P – P_i

 P_i –x = a –x⸫

P_i = a

وبالتعويض في المعادلة (11) نحصل على :

 ومنها نحصل على قيمة K

(ب) تفاعلات الرتبـة الثانيـة في المحاليل

ومن أمثلتها التميؤ القاعدي للإسترات وتفاعل هاليدات الألكيل مع الأمينات واتحاد أيونات الأمونيوم والسيانات لتكوين اليوريا وكذلك أسترة الأحماض العضوية فمثلاً في حالة تميؤ خلات الإيثيل بواسطة أيونات الهيدروكسيد

CH₃CH₂COOC₂H₅ + OH^–  → CH₃CH₂COO^– + C₂H₅OH

ويحضر مخلوط التفاعل بخلط محاليل مائية معلومة التركيز من خلات الإيثيل وهيدروكسيدالباريوم لكي تعطي تركيزات أزلية تساوي a من الأستر ، b من القاعدة ، وتقاس سرعة التفاعل بأخذ عينات من المخلوط وتخفيفها بواسطة الماء البارد لإيقاف التفاعل ثم معايرتها بحمض قياسي.