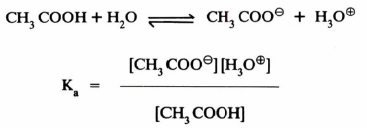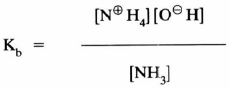حموضة الاحماض وقاعدية القواعد

حموضة الاحماض وقاعدية القواعد

– في هذا الموضوع سوف نتكلم عن حموضة الاحماض وقاعدية القواعد وكيف يمكن التفرقة بين الأحماض القوية والضعيفة وكذلك بين القواعد القوية والضعيفة.

أولاً/ تعريف الأحماض والقواعد

– تم تعـريف الأحماض والقـواعـد بعـدة تـعـريفـات:

(1) تعريف أرهينيوس للأحماض والقواعد

– فلقد عرف العالم أرهينيس Arrhenius الأحماض بأنها تلك المركبات التي لها قدرة على إعطاء أيون هيدروجين (بـروتـون ⁺H) في المحلول بينها القواعد هي تلك المركبات القادرة على إعطاء أيون هيدوكسيل OH في المحلول .

– ويعتبر الكيميائيون هذا التعريف للأحماض والقواعد كافياً إذا أجرى التفاعل في وسط مائي وهو لا يتوفر لكثير من التفاعلات العضوية .

(2) تعريف برونستيد – لوري للأحماض والقواعد

– يعتبر تعريف برونستيد ـ ولورى Bronsted-Lowry للأحماض والقواعد أكثر شمولاً إذ تعرف الأحماض بالمواد القادرة على إعطاء بروتون (مثل: HNO₃ , HC1) والقواعد بالمواد القادرة على ضم بروتون (مثل: OH, NH₃^–)

(3) تعريف لويس للأحماض والقواعد

– وبـالـرغم من أن كثيراً من تفاعلات الأحماض والقواعد تخضع لانتقال أيون هيدروجين من الحمض إلى القاعدة إلا أنه وجد أن بعض أنواع هذه التفاعلات لا يحدث فيها انتقال بروتون .

– ومن هذا المنطلق فقد طور العالم لويس Lewis الأحماض والقـواعـد فقـال بأن الأحماض هي تلك المواد القادرة على ضم زوج من الإلكترونات (مثل: AlCl₃ , FeCl₃) بينها القواعد هي المواد التي لها قدرة على إعطاء زوج من الإلكترونات (مثل: OH, NH₃^–)

من هذا نرى أن هذه التعريفات للأحماض والقواعد وإن اختلفت شكلاً فإنها تتفق جوهـراً في كون الأحماض مواد فقيرة إلى إلكـتـرونـات بينها القواعد مواد غنية بالإلكترونات.

ثانياً/ حموضـة الأحمـاض

– تتأين الأحماض العضوية في المحاليل المائية بانتقال بروتون منها إلى المذيب ويكون هذا التفـاعـل في حالة اتزان Equilibrium يمكن معه قياس ثابت الاتزان (K_a).

– ويسمى ثابت الاتزان (التأين) للأحماض العضوية الضعيفة بثابت الحامضية (Acidity constant (K_a .

– وتعتبر قيمة ثابت الحموضة مقياساً لقوة الحمض ويمكن حسابه بصفة عامة من المعادلة التالية:

 

وكلما زادت القيمة العددية لثابت الحمض كلما دل ذلك على زيادة حموضية الحمض.

–  وتبين المعادلة التالية ، كيفية حساب ثابت الحامضية لحمض الخل:

وقد حذف تركيز الماء في مقام المعادلة الأخيرة نظرا لبقائه ثابتاً تقريباً.

– ولقد وجد من التجارب العملية أن قيمة K_a لحمض الخل تساوي ^5-10 × 1.8 وتجنباً لكتابة أرقام كثيرة تشتمل أيضاً على قوة سالبة للعدد عشرة فقد وجد أنه أسهل من الناحية العملية تبسيط قيمة K_a إلى ثابت آخر يسمى pK_a وتربطها العلاقة التالية:

 

 فتصبح قيمة pk_a لحمض الخل 4.76

– ويجب ملاحظة أن حموضة الحمض في حالة استخدام pK_a كمقياس للحامضية، أن الحامضية تزداد كلما صغرت قيمة pK_a .

– وتتأثر قيمة K_a أو pK_a بنوع المذيب المستخدم وكذلك بعوامل أخرى مثل الفعل التحريضي وظاهرة الطنين.

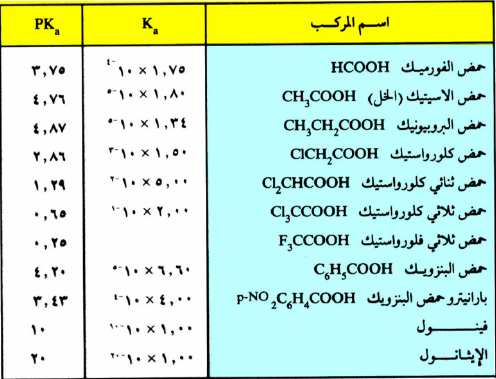
– ويبين الجدول التالي  لثوابت الحامضية لبعض الأحماض الكربوكسيلية .

 

ثالثاً/  قاعـديـة القواعـد

– يعتبر زوج الإلكترونات الحر على ذرة النيتروجين في النشادر مسؤولاً عن خواص القاعدة.

– والنشادر قاعدة ضعيفة تمتزج امتزاجاً تاماً بالماء وتتفاعل معه لتكون أيون الأمونيوم الموجب وأنيون الهيدروكسيل .

 

– وتسلك القواعد الأخرى مثل الأمينات عند تفاعلها مع الماء مسلكاً مشابهاً مع اختلاف في قاعدية المحلول وفقاً لنوع المادة المذابة.

– ومن الملاحظ أن التفاعل أعلاه تفاعل اتزان يمكن معه إيجاد ثابت الاتزان والذي يعبر عن ثابت القاعدية (Basicity constant(K_b وفقا للمعادلة التالية مع اعتبار أن تركيز الماء ثابت خلال التفاعل .

 

– ولقد وجد من التجارب العملية أن قيمة K_b للنشادر تساوي ^5-10 × 2 عند درجـة  25م^o

– وبصفة عامة فإن القاعدية لأي مركب تزداد كلما زادت القيمة العددية للثابت K_b .

– كذلك يمكن التعبير عن القاعدية بالثابت pK_b والذي يمكن حسابه من المعادلة التالية كما يلي:

 

– وفي حالة استخدام الثابت pK_b فإن القاعدية تزداد كلما صغرت القيمة العددية لهذا الثابت.

– والجدير بالذكر أن هناك تلازماً بين قيمة pK_a ، وقيمة pK_b في المحاليل المائية عند درجـة 25 م^o. وعليه يمكن من معرفة أحدهما الحصول على قيمة الآخر من المعادلة كما يلي:

 

– ومن الملاحظ أن المعادلة السابقة تعبر أيضاً عن قيمة الرقم الهيدروجيني pH للمحلول المائي. والذي يساوي مقلوب لوغاريتم تركيز الهيدروجين في المحلول .

– وعلى ذلك فإن المحاليل المتعادلة تكون قيمة pH فيها مساوية 7. بينما في المحاليل الحامضية تكون القيمة أقل من 7 وأكبر من 7 في المحاليل القاعدية .

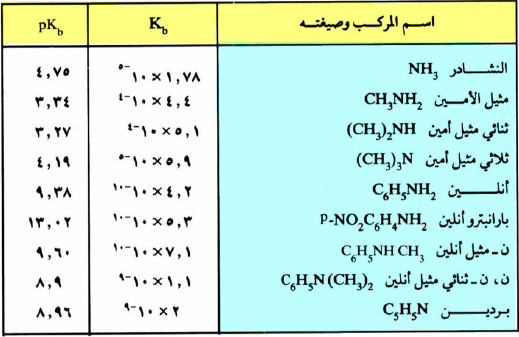
– ويبين الجدول  التالي ثوابت القاعدية لبعض المركبات العضوية .

المراجع:

كتاب ميكانيكية التفاعلات العضوية ، تأليف/ د.سالم بن شويهان ، د. إبراهيم بن محمود النجار ، د. حمد بن عبدالله اللحيدان ، الرياض – جامعة الملك سعود – الطبعة الثانية 2003م